La Geometría Elemental nos permite determinar el punto de observación desde el que una estatua situada sobre un pedestal puede ser contemplada de forma óptima. Ese punto será aquel desde el cual nuestro ángulo visual de la estatua sea máximo. En realidad hablamos de un punto porque pensamos que la observación la hacemos de frente, pero hay infinitos puntos desde los que la estatua puede ser observada bajo ese mismo ángulo máximo.
Para determinar ese punto utilizaremos propiedades de la medida de los ángulos inscritos en la circunferencia.
En la circunferencia podemos distinguir dos tipos de ángulos, según la posición del vértice en la misma: ángulo inscrito y ángulo central.
El ángulo inscrito en la circunferencia tiene su vértice en la circunferencia y sus lados son cuerdas. Por ejemplo el ángulo (ABA’) = b de la figura.
El ángulo central de la circunferencia tiene el vértice en el centro, C, de la circunferencia y sus lados son radios. Ejemplo: ángulo (ACA’) = c de la figura
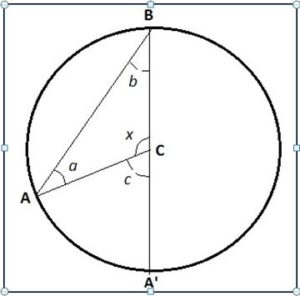
Las medidas de estos ángulos están relacionadas de la siguiente forma: Si un ángulo inscrito en una circunferencia abarca un arco AA’ de la misma y un ángulo central abarca el mismo arco, entonces el ángulo inscrito mide la mitad del arco que abarcan sus lados, es decir, la mitad del ángulo central correspondiente:
2(ángulo ABA’) = ángulo ACA’
Lo podemos comprobar en el caso de que uno de los lados del ángulo inscrito sea un diámetro de la circunferencia como se indica en la figura.
En este caso el triángulo ABC es isósceles ya que dos lados son radios de la circunferencia.
Por lo tanto: a = b y a + b + x = 180º ⇒ 2b + x = 180º y como también se cumple (por ser A’CB un ángulo llano que c + x = 180º, se obtiene que 2b = c.
Con este resultado se puede abordar el problema que hemos planteado al principio, en un ejemplo con datos numéticos:
Problema.- En un parque hay una estatua de 2m sobre un pedestal de 2m de altura. Una persona tiene los ojos a 1’40m del suelo ¿A qué distancia horizontal del pie del pedestal se debe colocar el paseante para observar la estatua bajo el mayor ángulo posible?
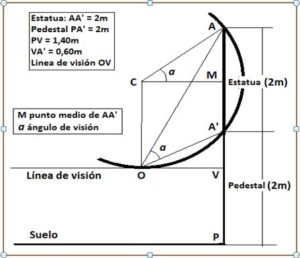
Respuesta: Supongamos que AA’ es la estatua y PA’ el pedestal. La persona que desea observar la estatua desde el suelo teniendo la altura de sus ojos a 1,40m del suelo se mueve en línea OV paralela al suelo horizontal.
1.- Supongamos que observamos la estatua desde el lado izquierdo, según de figura.
2.- Si consideremos el conjunto de todas las circunferencias que pasan por A y A’, es decir, las que tienen a AA’ como cuerda, observamos lo siguiente:
- Desde cualquier punto de cada circunferencia se observa AA’ con el mismo ángulo
- Cuanto mayor sea el radio de la circunferencia desde a que observemos AA’ menor será el ángulo bajo el que la observamos
- Las circunferencias que pasan por A y A’ y están por encima de la línea de visión OV no afectan, porque desde sus puntos el observador no puede contemplar la estatua.
- El resto de las circunferencias cortará a la línea visión en dos puntos, salvo una que será tangente a la misma, esta será la circunferencia de menor radio desde la que podemos observar AA’ (Y, por tanto, la que nos proporcione mayor ángulo de observación de la estatua AA’)
El radio de esta circunferencia que pasa por A, A’ y por el punto de tangencia O, de la circunferencia con la línea de visión OV, será:
Radio = AP – AM – VP = 4 – 1 – 1,40 = 1,60m
El ángulo de observación a es un ángulo inscrito en la circunferencia AA’O de centro C, que abarca la cuerda AA’. Este ángulo será la mitad del ángulo central que abarca la misma cuerda y que es a del triángulo rectángulo AMC. La distancia OV la mediremos sobre ese triángulo con el teorema de Pitágoras:
![]()
El ángulo a que proporciona mejor contemplación de la estatua será:
a = arcsen (AM/AC) = arcsen (1/ 1,60) = 38º40’ 56’’