
En la Geometría Griega se llamaban Problemas Planos a las cuestiones que podían resolverse trazando rectas y circunferencias. Es decir, eran los problemas que podían resolverse mediante el uso de la regla y el compás. Era una Geometría construible y exacta en la que las demostraciones de los diferentes teoremas se podían dibujar con la regla y el compás, que eran considerados los instrumentos de dibujo más precisos.
La circunferencia fue la primera línea curva plana que apareció en la geometría griega. No obstante, los griegos también aceptaron como curvas geométricas, aunque no fueran construibles con regla y compás, la elipse, la parábola y la hipérbola, porque las tres se podían generar por intersecciones de un plano con un cono. El resto de las curvas que no podían construirse con regla y compás quedaron fueray del reino de Geometría Pura y las llamaron curvas mecánicas, las cuales se generaban por el movimiento de un punto bajo ciertas condiciones. A los ojos de los griegos estas curvas carecían de la pureza y de la belleza matemática de las curvas geométricas.
Algunos geómetras griegos estudiaron curvas mecánicas por diversos motivos, en primer lugar, por la curiosidad investigadora, en segundo, lugar para tratar de resolver con ellas alguno de los tres problemas clásicos griegos que eran: la cuadratura del círculo, la duplicación del cubo y la trisección del ángulo, los cuales se resistían a ser resueltos con la regla y el compás y, por último, algunas curvas se estudiaron por la carga simbólica que tenían en las culturas antiguas.
En este contexto aparecieron, hacia el siglo V a. de C, curvas como la Cuadratriz de Dinóstrato que permitía resolver los problemas de la trisección del ángulo y la cuadratura del círculo; en el siglo III a. de C. la Concoide de Nicomedes y en el siglo II a. C. la Cisoide de Diocles. Todas esas curvas resolvían los mismos problemas. En el siglo III a. de C. Arquímedes (287-212 a. de C.) estudió la Espiral Uniforme, que era una curva que evocaba el infinito y trisecaba ángulos.
Arquímedes escribió el libro De las espirales, en el que estudió, con rigor euclidiano, las propiedades de la Espiral, la cual era una curva mecánica, y demostró numerosos teoremas verdaderamente interesantes sobre las propiedades de esta curva. De las espirales es un libro de lectura difícil, hasta el punto que muchos matemáticos de los siglos XVII y XVIII lo llegaron a considerar incomprensible e incluso erróneo, pero, con el cálculo infinitesimal, se pudo demostrar que los teoremas del libro era ciertos y comprobar de forma patente la genialidad de Arquímedes.
Arquímedes define su espiral de la siguiente forma:
Si permaneciendo fijo uno de los extremos de una recta [segmento], ésta gira con velocidad uniforme hasta volver a la posición inicial y un punto, también con velocidad uniforme, recorre al mismo tiempo, la recta que gira a partir del extremo fijo, este punto describe una espiral en el plano.
Dicho de forma intuitiva, la Espiral sería la trayectoria sobre el plano de una hormiga que camina con velocidad uniforme sobre una varilla fija por uno de sus extremos, O, mientras la varilla que gira sobre el plano con velocidad uniforme.
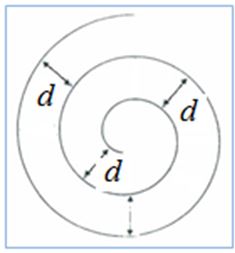
La primera característica de la Espiral de Arquímedes es que la distancia entre dos espiras consecutivas es constante, ya que el desplazamiento del punto P sobre la semirrecta y la rotación de la misma alrededor de su extremo, O, tienen velocidad constante.
La ecuación de la Espiral es fácilmente expresable en coordenadas polares con las que cada punto P del plano queda determinado por su distancia al origen O, que es r, y el ángulo, ϑ, que forma OP = r con la parte positiva del eje horizontal, como se muestra en la figura:
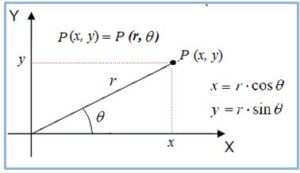
La ecuación de la espiral de Arquímedes es fácil expresarla en coordenadas polares, ya que la distancia de un punto de la espiral al origen es directamente proporcional al ángulo girado y tendrá, en coordenadas polares, la ecuación siguiente:
r = a·ϑ
En coordenadas paramétricas se expresará:
x = a·ϑ cos ϑ y = a·ϑ sen ϑ; ϑ ∈[0,∞)
La distancia entre espiras, que es la distancia entre dos giros sucesivos, será.
r1 = a·(ϑ+2π), r2 = a·ϑ ⇒ d = r1 – r2 = a·2π
La obra De las Espirales contiene veintiocho proposiciones que requieren el uso del Cálculo Infinitesimal, que Arquímendes resolvió utilizando el método de Exhaución de Eudoxo casi dos mil años antes de que se inventara el Cálculo. He aquí dos de ellas:
Proposición 24.- El área barrida por el radio de la espiral en su primera revolución es la tercera parte del área del círculo cuyo radio es el radio final de la revolución…
Proposición 25.- El área barrida en la segunda revolución está en razón 7/12 con el círculo cuyo radio es la posición final del radio vector»
Con el estudio de la Espiral el sabio de Siracusa intentó tres cosas la primera estudiar una curva con una gran carga simbólica. La Espiral expresaba la fuerza vital, el crecimiento y, como se alejaba del origen, O, siguiendo siempre la misma pauta, muchos creían que representaba el ciclo del nacimiento y de la vida como una la sucesión creciente e indefinida de acontecimientos. La segunda era dignificar, con estudio amplio y monográfico, las propiedades matemáticas que tenía una curva mecánica, las cuales no eran menos interesantes que las que tenían las curvas geométricas (las cónicas). Pero, además, la Espiral permitía resolver un: la trisección del ángulo. Arquímedes, con la espiral uniforme, proporcionó un método para dividir un ángulo en tres partes iguales, y en general en n partes iguales.
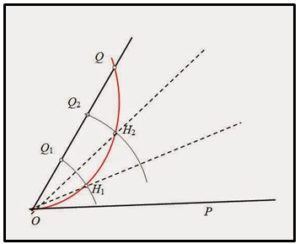
Para trisecar el ángulo QOP siguen los siguientes pasos:
1.- Colocar el vértice O del ángulo con el origen de la espiral.
2.- Dividir el segmento OQ (Q es el punto de corte de lado del ángulo con la espiral) en tres partes iguales por los punto Q1, Q2.
3.- Trazar, haciendo centro en O arcos de circunferencia hasta que corten a la espiral los punto H1, H2.
4.- Las semirrectas OH1 y OH2 dividen al ángulo QOP en tres partes iguales.
Si hubiéramos dividido el segmento OQ en cinco partes iguales podríamos haber dividido el ángulo en cinco partes iguales y si lo hubiéramos dividido en n partes el ángulo se habría dividido en n partes.




