Los problemas de los que nos vamos a ocupar tienen su punto de partida en una carta privada que el matemático francés P. Fermat (1601-1675) le envió al físico italiano E. Torricelli (1608-1647) en la que le proponía la resolución de un problema que podría plantearse así:
Problema (Fermat-Torricelli): Dados tres pueblos A, B y C, (no alineados) se desea determinar un punto P en el que se debe situar un almacén de suministros para que la suma de distancias de los tres pueblos al almacén: PA + PB + PC sea mínima.
El problema fue resuelto por Torricelli, aunque su demostración fue publicada en 1659 por su pupilo V. Viviani (1622-1703), también B. Cavalieri dio otra solución y el resultado es el siguiente:
Los tres pueblos forman un triángulo ABC y el punto P se llama Punto de Fermat. Y, en un triángulo cuyos ángulos son menores de 120º, el punto P cumple la condición siguiente:
ángulo (APB) = ángulo (BPC) = ángulo (CPA) = 120º.
Torricelli demostró, por procedimientos puramente geométricos de la forma que mostramos a continuación, que si el punto cumplía esa condición la suma de distancias PA + PB + PC era mínima
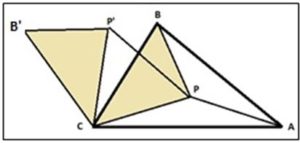
Tomemos un punto arbitrario P interior al triángulo, uniendo P con los vértices A, B y C, el triángulo ABC queda dividido en los tres triángulos: PAB, PBC y PCA.
1.- Con centro en el vértice C giremos el triángulo PBC un ángulo de 60º y se transforma en el triángulo P’B’C.
2.- Con este giro se puede observar que, dado que el giro mantienen las distancias, que BP = B’P’ y que CP = CP’ = PP’, ya que, al girar PC 60º, el triángulo PP’C es equilátero.
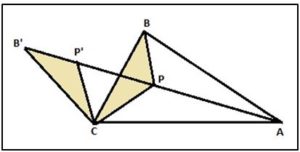
3.- Por lo tanto: PA + PB + PC = PA + PP’ + P’B’ y esta suma será mínima cuando los puntos A, P, P’ y B’ estén alineados.
4.- Si el ángulo BPC = 120º, entonces P’ está alineado con A y P ya que ángulo BPP’ = 60º (BPP’+ APB =180º) y B’ está alineado con P y P’, ya que ángulo B’P’C = 120º y ángulo CP’P = 60º y la suma de los dos da un ángulo llano. Por lo tanto, los puntos A, P, P’ y B’ están alineados, que es lo que queríamos probar.
Si el triángulo ABC un ángulo ≥ 120º el punto de Fermat se sitúa en el vértice correspondiente a ese ángulo.
Un problema de corte parecido está recogido en el teorema de Viviani que lo podemos plantear así:
Problema (Viviani): Tres pueblos A, B y C están unidos por tres carreteras rectilíneas AB, BC y CA que forman un triángulo equilátero. ¿Dónde se debe construir una almacén P para que la suma de las distancias del almacén a las tres carreteras sea mínima?, es decir: d(P,AB) + d(P, BC) + d(P, CA) sea mínima
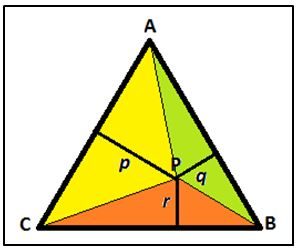
Si ABC es un triángulo equilátero y P es un punto cualquiera interior al triángulo y lo unimos con sus vértices, el triángulo ABC queda dividido en tres triángulos: PAC, PAB y PBC de base L y de alturas respectivas (desde P) p, q y r. Y tenemos que:
Area (ABC) = Area (PAB) + Area (PBC )+ Area (PCA) ⇒
L· h/2 = L· p/2 + L·q/2 + L· r/2 ⇒ h = p + q + r
Y esto ocurre con todos los puntos interiores del triángulo equilátero. La suma de las perpendiculares a los tres lados del triángulo desde un punto P interior es constante e igual a la altura del triángulo equilátero. Luego es indiferente la elección del punto P donde ubicar el almacén. Lo que es, en esencia, el teorema de Viviani, que dice:
Teorema de Viviani: En un triángulo equilátero la suma de las perpendiculares trazadas desde un punto interior cualquiera a los lados del triángulo es igual a la altura del mismo.
A partirdel teorema de Viviani podemos observar lo siguiente:
1.- Si p, q y r son las perpendiculares a los lados del triángulo equilátero desde un punto P interior del mismo entonces p + q + r = h
2.- Si se trazan desde P rectas u, v y w que no sean no perpendiculares a los lados del triángulo equilátero la suma de las mismas será mayor que h. (u + v + w > h)
3.- Las perpendiculares a los lados del triángulo forman entre si ángulos de 120º.
A partir de estos resultados se puede probarel teorema de Fermat- Torricelli de la siguiente forma:
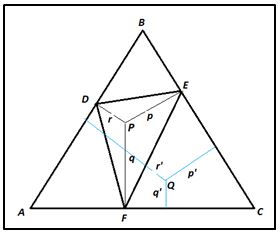
Consideremos un triángulo cualquiera DEF y un punto P el punto desde el que las líneas que los unen con sus vértices forman entre si ángulos de 120º. Entonces:
1.- Las perpendiculares a esas líneas que pasan por los vértices del triángulo forman un triángulo equilátero ABC.
2.- Si desde otro punto Q interior cualquiera se trazan las perpendiculares a los lados del triángulo equilátero ABC: p’ + q’ + r’ = p + q + r
3.- Si unimos Q con QD + QE + QF > p’ + q’ + r’ = p + q + r.
4.- Como esto vale para cualquier Q del triángulo ABC y, en particular para los puntos de DEF ⇒ que el punto P en el que PD, PE y PF se cortan en ángulo de 120º es aquel que hace que la suma de distancias sea mínima. Lo que constituye una comprobación del Teorema Fermat-Torricelli.