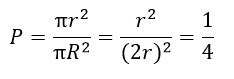La palabra paradoja proviene del latín paradoxa, que literalmente quiere decir contrario (para) la opinión (doxo) común. Se presentan paradojas en lógica y en muchos temas de las matemáticas como el infinito, aritmética, geometría, probabilidades, etc. Estudiaremos una paradoja de probabilidades propuesta por el matemático francés Joseph Bertrand (1822-1900) en su libro Calcul des probabilités (1888). Las paradojas suelen colocarnos en la perplejidad, y la imposibilidad aparente porque nos muestran un callejón sin una salida de la lógica. Algunas, como la paradoja de Russel o paradoja del barbero, ponen de manifiesto una contradicción, la de paradoja de Teseo o paradoja de reemplazo presenta la necesidad de profundizar en la identidad, la paradoja de Banach- Tarski o paradoja del guisante y el Sol nos muestra que situaciones paradójicas contrarias al sentido común pueden ser demostradas dentro de una teoría matemática válida.
Las paradojas suelen aparecer y se formulan en escenarios complejos de desarrollo y expansión de alguna parcela particular de la ciencia y ponen de manifiesto situaciones que no pueden solucionarse ni aclararse con los conceptos y argumentos tradicionales al uso. En el caso de Bertrand, la paradoja surgió por no disponer de una definición precisa de experimento aleatorio y de variable aleatoria en la formulación del problema.
El problema (Paradoja) de Bertrand: Consideremos una circunferencia, C, y una cuerda AB trazada al azar sobre ella ¿Cuál es la probabilidad de que esta cuerda tenga una longitud mayor que el lado del triángulo equilátero inscrito en la circunferencia?
El problema está claramente planteado, pero ¿cómo se traza al azar la cuerda AB, que une dos puntos distintos de la circunferencia? Precisamente en la elección del método para trazarla y en las propiedades del infinito está la paradoja. Bertrand propuso tres modos de calcular la probabilidad de que la cuerda tenga una longitud mayor que el lado del triángulo equilátero inscrito en la circunferencia que tenían tres resultados diferentes.
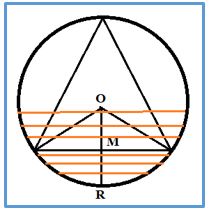
PRIMERO: Elegimos la cuerda AB por su distancia, d al centro de la circunferencia
La distancia del centro de la circunferencia a la cuerda es la longitud de la perpendicular que va del centro del dentro a la cuerda. La distancia varía de cero a R y las cuerdas cuyas distancias son mayores que el lado del triángulo equilátero van de O a M. Pero OM es la mediana del triángulo y es igual a la mitad del radio de la circunferencia en la que está inscrito el triángulo equilátero, por lo tanto: OM = 0R/2. Como esta relación se conserva en cualquier dirección que tracemos la cuerda la probabilidad de que la cuerda sea mayor que el lado del triángulo equilátero ser 1/2.
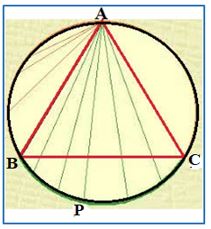
SEGUNDO: Partimos de un punto A situado sobre la circunferencia, y, desde él, elegimos un punto cualquiera, P, también sobre de la circunferencia. Si ABC es un triángulo equilátero, las cuerdas AP solamente serán mayores que el lado del triángulo cuando P esté entre A y C. Como el arco BC es la tercera parte de la circunferencia, la probabilidad de que sea AP > AB será 1/3 . Por lo tanto, con este sistema de elección de la cuerda, la probabilidad de que, la cuerda elegida sea mayor que el lado del triángulos equilátero inscrito será1/3 .
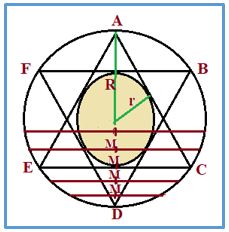
TERCERO: Elegimos la cuerda teniendo en cuenta la posición de su punto medio M. Si el triángulo equilátero AEC está inscrito en una circunferencia de radio R, Las cuerdas paralelas al lado EC tienen su punto medio, M, en el diámetro perpendicular AD. Las cuerdas serán mayores que el lado del triángulo equilátero cuando sus centros estén dentro del circulo interior de radio r de la figura, que es la apotema del triángulo equilátero y, por tanto, la mitad de su radio R. Por consiguiente, la probabilidad será el cociente de las áreas de los de los círculos: