Sabemos que la distancia más corta entre dos puntos es la línea recta. Pero, en muchas ocasiones, la línea recta es una trayectoria que no podemos seguir. El camino que recorre una hormiga sobre una pelota no puede ser una línea recta. Si la superficie en la que se mueve la hormiga fuera un cilindro de revolución, la línea de mínima distancia entre dos puntos (geodésica) podría ser: una generatriz (si los puntos estuvieran en una recta paralela al eje, una circunferencia (si los dos puntos estuvieran en un plano perpendicular al eje) o un trozo de una hélice cilíndrica que los una en otro caso
A continuación presentamos en un caso sencillo de geometría no euclidiana sobre un plano con una métrica distinta a la que utilizamos habitualmente. La métrica de nuestro plano está relacionada con la distancia recorrida por un taxista o un peatón en una ciudad donde las calles sólo tienen dos orientaciones: Norte-Sur y Este-Oeste. La medida que se utiliza se llama Métrica Manhattan o Métrica del Taxista, en ella lla consideraremos que las cuadrículas están formadas por cuadrados y que la trayectoria no puede ser siempre una línea recta.
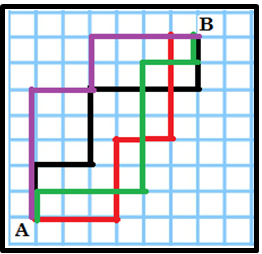
El taxista medirá la distancia entre dos puntos A y B contando el número de manzanas que ha de recorrer para ir de un punto a otro. Entendemos que la mínima distancia entre A y B será el número de manzanas que recorre el taxista sin hacer retrocesos. En la figura la distancia mínima que tiene que recorrer un peatón es de 13 manzanas (6 en horizontal y 7 en vertical), por tanto, 13 unidades es la distancia mínima. Pero se pueden hacer diferentes trayectos entre A y B con esa distancia; de hecho, los cuatro recorridos de la figura tienen la misma distancia: 13u. Mientras que la línea recta (que no es ningún recorrido posible) tendría una distancia de:
![]()
En un plano con la métrica de Métrica Manhattan hay muchas trayectorias que unen dos puntos A y B que tienen la mínima distancia. Si tomamos como cuadrícula en el plano cartesiano, dos puntos A(a, b) y B(a’, b’) tienen una distancia, según la Métrica Manhattan: |a – a’| + |b – b’|. Es decir, la suma de los valores absolutos de las diferencias de sus coordenadas.
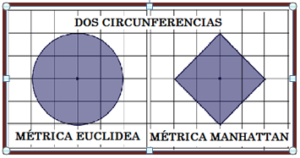
Esta métrica puede presentar algunas aparentes paradojas, ya que si observamos la figura 2, las cuatro líneas quebradas que unen los vértices opuestos, A y B, del cuadrado miden lo mismo. Exactamente el doble del lado del cuadrado: 2L.

Pero también podemos observar que, a medida que cuadrícula del cuadrado se hace más fina (los cuadraditos cada vez más pequeños), la línea quebrada se aproxima más y más a la diagonal hasta confundirse con ella. Como la línea quebrada mide 2L, podemos concluir que la diagonal del cuadrado también medirá 2L, lo que absurdo. La diagonal de un cuadrado no puede ser igual al doble de su lado, porque la recta es la distancia más corta entre dos puntos y porque el teorema de Pitágoras dice que la diagonal mide:
![]()
Lo paradójico de esta situación se debe a que estamos razonando con dos métricas diferentes que unimos sin ninguna justificación, pero, además, no aplicamos debidamente la noción matemática de límite que afirma que una magnitud variable x tiende hacia un valor límite a, si a medida que los valores de x se aproximan al número a, el valor absoluto de la diferencia (x – a) puede llegar a ser más pequeño que cualquier número positivo dado, ε, por pequeño que sea.
En el ejemplo paradójico, x sería la longitud de las líneas quebradas, que tiene valor constante 2L, y a sería la longitud de la diagonal AB (también constante). Como x es constante, la diferencia (x – a) es también constante y no se puede aplicar la definición de límite, porque las magnitudes no satisfacen las condiciones de la definición y al aplicarlo se llega a un absurdo.




