SOBRE LA CARDINALIDAD DE UN CONJUNTO Y SU DIMENSIÓN

Se llama cardinal de un conjunto al número o cantidad de elementos que contiene. Cuando el conjunto es finito el cardinal es un número natural. Cuando el conjunto es infinito, como lo es el conjunto de los números naturales, el cardinal ya no es un número. El matemático alemán G. Cantor (1845-1918) tuvo una idea que le permitió evaluar, no cuantos elementos tenía un conjunto infinito, sino si dos conjuntos A y B tenían la misma cantidad de elementos. La idea fue asociar a cada elemento de A un único elemento de B sin que quede en B ningún elemento desemparejado. En matemáticas se dice que dos conjuntos A y B tienen la misma cantidad de elementos si es posible establecer entre ambos una correspondencia biyectiva.

Esta manera natural de comparar conjuntos llevó a situaciones paradójicas. Cuando se pretendía comparar conjuntos infinitos. Así, cuando comparamos el conjunto de los números naturales N = {1, 2, 3,…} con el de los pares P = {2, 4, 6,…}, se observa fácilmente que el conjunto P está contenido en N. Sin embargo, cuando tratamos de emparejar los elementos de P con los de N, asociamos a cada elemento de N su duplo en P (correspondencia biyectiva  entre P y N), es decir:

1  →  2,     2  →  4,     3  →  6,     4  →  8,     5  →  10,

 Con esa correspondencia ni en P ni en N quedan elementos sin emparejar, por lo que ambos conjuntos tienen la misma cantidad de elementos, lo que se resume diciendo que ambos conjuntos son infinitos coordinables. Richard Dedekind (1831-1916) utilizó esta pintoresca propiedad de los conjuntos infinitos diciendo que un conjunto era infinito si tiene un subconjunto propio coordinable con él.

Un conjunto es infinito contable (o infinito  numerable) si existe una correspondencia biyetiva entre los elementos del conjunto y los del conjunto N de los números naturales.  Cantor publicó en 1874 un artículo Sobre una propiedad característica de la totalidad de los números reales algebraicos donde demostraba que los números racionales eran numerables, es decir que había tantos números racionales como naturales.

Cuando George Cantor estudió los conjuntos infinitos continuos probó que el segmento (0,1) de la recta real tenía tantos elementos como recta real positiva completa y, por consiguiente, tantos elementos como la recta real completa. Resultado que puede probarse con un modelo gráficamente como se muestra en la figura adjunta. En la que a cada recta que pasa por el punto P y  corta al segmento  en un punto A, asocia a este punto otro A’ de la recta real positiva de manera única. Así, a los puntos A, B, C… de (0,1) les corresponden los puntos  A’, B’, C’… de (0,∞) y recíprocamente.

Las investigaciones de Cantor sobre los conjuntos infinitos dieron un paso más cuando probó el segmento unidad (0,1) tenía tantos  elementos como el cuadrado de lado unidad (0,1)x(0,1)  y tantos como en el cubo (0,1)x(0,1)x(0,1). Lo que chocaba, en principio,  de la imagen intuitiva de que los granos de arena contenidos en un metro cúbico  pudieran extender en una fina capa sobre un metro cuadrado y alinearse en un segmento de longitud unidad. Chocaba con la noción de dimensión como veremos a continuación.

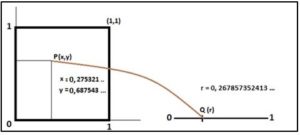
A título de ilustración esbozamos la construcción de la correspondencia  biyectiva entre el segmento retilíneo (0,1) y el cuadrado (0,1)x(0,1) que se puede establecer con facilidad. La idea básica consiste en lo siguiente: Tomemos, tal y como se ve en la figura,  el punto del cuadrado

P(x, y) = (0,275321..,  0, 687543 ..)

Y le hacemos corresponder: Q(r) = Q(0,267857352413…), dónde r se ha obtenido escribiendo alternativamente las cifras decimales de las coordenadas del punto P. Esta correspondencia sería biunívoca si la representación de cada número en forma decimal fuera única.

(Debemos observar que, como hay números que tienen dos expresiones decimales diferentes, como r = 0,1 = 0, 0999 … Para solucionar esta pega y hacer que la correspondencia anterior sea biyectiva la modificaremos  un poco lconsiderando que el cero no es cifra independiente, esto es, que cuando encontremos un cero en la expresión decimal de una de las coordenadas de P, no intercalaremos solamente el cero, sino el grupo de cifras que va desde ese cero hasta la primera cifra significativa. Así, al punto P(x, y) donde x = 0,10109017 …  e  y = 0,50500392 …, le corresponde: Q(r) donde r = 0,1 5 01 05 09 003 01 9 7 2…)

Con este descubrimiento, el infinito no afectaba solamente al hecho de que una parte del conjunto infinito tenía tantos elementos como el conjunto entero, que mostraba clara contradicción con el principio lógico de que el todo es mayor que la parte, sino que lardinalidad de los conjuntos infinitos continuos entraba en conflicto con en concepto de dimensión: el segmento (0,1), que tenía dimensión uno, longitud uno y área cero, tenía el misma cantidad de elementos que  el cuadrado (0,1)x(0,1) dimensión dos  y área unidad.

B. Riemann (1826 – 1866) había definido la dimensión de una variedad como como el número de variables necesarias para determinar la posición de un punto de la misma. Así, fijado un origen O,  para determinar un punto en la recta (dimensión 1) basta con un número real r, para, para determinarlo en el plano (dimensión 2)  hacen falta dos números reales (x, y), en el espacio  hacen falta tres (x, y, z). Pero Cantor demostraba que para cada punto P (x, y) del plano se le podía identificar con un número r.

¿Cómo podía ser que un segmento rectilíneo de área cero tuviera tantos elementos como un cuadrado de área unidad o un cubo de volumen uno?¿Qué aporta la dimensión a la cantidad de elementos que tuene un conjunto?

Este problema fue planteado en una carta de Cantor a R, Dedekind (1831-1916)   en 1877. Dedekind observó que la correspondencia tal que a cada punto P (x, y) le hacía corresponder un punto Q(r) en la recta real era biunívoca, pero no era continua, esto significaba que a puntos próximos a P no les debían corresponde puntos próximos a Q y recíprocamente. Dedekind formuló la conjetura de invariancia de la dimensión por aplicaciones biyectivas bicontinuas, llamadas homeomorfismos.

Hablando sin excesivo rigor, podemos decir que la correspondencia que hemos establecido entre (0,1) y el cuadrado (0,1)x(0,1) es biyectiva,  pero no es continua y rompe la propiedad de  proximidad topológica, esto es, a puntos próximos del primer espacio no les corresponden puntos próximos en el otro espacio produciendo rupturas (o discontinuidades). Esta conjetura la intentaron probar muchos matemáticos, pero  la demostración definitiva  realizó en 1911 el matemático intuicionista holandés L.E.J. Brouwer (1881-1966).

Y, del mismo modo que las correspondencias biyectivas entre dos conjuntos preservan la cantidad, y los homomorfismos trasladan propiedades de las operaciones algebraicas entre dos conjuntos, los homeomosfismos mantienen las vecindades y sólo se pueden establecer homeomorfismos entre espacios de la misma dimensión.

El teorema de invariancia de la dimensión lo podemos formular por homeomorfismoade la siguiente forma:

Si un abierto U de Rⁿ  es homeomorfo a un abierto V de R^m,  entonces n = m .