La Geometría de Euclides (325-265 a. de C.) transmitió la idea de que todos sus postulados o axiomas eran evidentes. Realmente, la justificación de la veracidad de los postulados se apoyaba en que se podían verificar con una representación gráfica. Los postulados eran:
Postulado 1.– Se puede trazar una línea recta desde un punto hasta otro cualquiera.
Postulado 2.– Se puede prolongar una línea recta finita continuamente.
Postulado 3.– Se puede describir una circunferencia con cualquier centro y cualquier radio.
Postulado 4.– Todos los ángulos rectos son iguales.
Postulado 5.– Si una línea recta cruza otras dos líneas rectas forma ángulos interiores del mismo lado menores que dos ángulos rectos, entonces, si se continúan esas dos rectas indefinidamente, se cortan del lado en el que hay ángulos menores que los dos ángulos rectos.
Dejando de lado las repercusiones que tuvo la Geometría de Euclides como representación del espacio físico en sus más de veinte siglos de vigencia la geometría de los Elementos y, centrándonos en los aspectos puramente geométricos, que, seguramente, serían las preocupaciones de Euclides, señalaremos lo siguiente:
Los tres primeros postulados tienen carácter constructivo para para justificar el trazado rectas y circunferencias, justificando, de alguna forma, la tradición de geometría griega de la regla y el compás. El Cuarto Postulado señalaba el papel de los ángulos rectos como patrón o unidad para medir los demás ángulos.
Finalmente, el Quinto Postulado, que estaba redactado de forma algo más complicada, era un axioma de incidencia de rectas y fue conocido desde el siglo XVIII como el Axioma o Postulado de las Paralelas, el cuál comparte con los tres primeros cierta semejanza, ya que exige, por una parte, la existencia de unos puntos de intersección entre rectas, aunque, por otra parte, completa la definición 23 de los Elementos de rectas paralelas en la que dice:
Definición 23.- Son rectas paralelas las que estando en el mismo plano y siendo prolongadas indefinidamente en ambos sentidos no se encuentran una a otra en ninguno de ellos.
Esta definición de rectas paralelas no era la única conocida ni, al parecer, la más frecuentemente utilizada; era más natural la definición rectas paralelas por equidistancia, pero Euclides se decidió por el criterio, menos intuitivo de no intersección.
Es cierto que el Quinto Postulado era diferente de los otros cuatro y parecía que no era del agrado de Euclides, ya que trató de evitar su uso tanto como pudo. De hecho, no lo utilizó en las primeras veintiocho proposiciones de los Elementos y lo usó por primera vez en la:
Proposición 29.- La recta que incide sobre rectas paralelas hace los ángulos alternos iguales entre sí; y el (ángulo) externo igual al interno y opuesto; y los (ángulos internos del mismo lado iguales a dos rectos
En sus más de veinte siglos de reinado de la Geometría Euclidiana se buscaron formulaciones más sencillas y enunciados diferentes que unas veces incluían la noción de rectas paralelas y otras no. Desde el principio la coherencia que se apreciaba en la Geometría Euclídea llevó a la idea de que el Postulado de las Paralelas podía ser deducido a partir de los restantes y que, por lo tanto, podría ser redundante o superfluo. Los intentos de demostrar que era una consecuencia lógica de resto de los Postulados tuvo consecuencias importantes para el desarrollo de las matemáticas ya que se encontraron formulaciones equivalentes, se avanzó en el concepto de espacio y llevó a que en siglo XIX aparecieran las Geometrías no Euclidianas que supuso una renovación en la concepción de las matemáticas.
Algunos geómetras modificaron la definición de rectas paralelas de Euclides, como rectas no se encuentran por más que se prolonguen, y, aunque quedaba abierta la posibilidad de que fueran líneas asintóticas, en las que su distancia pudiera llegar a hacerse tan pequeña como se quisiera, sin llegar a juntarse, como ocurre con la hipérbola y su asíntota, optaron por la aquidistancia, como lo hizo Posidonio de Apamea (s. I a. de C.)
Dos rectas paralelas son equidistantes
Quince siglos después el jesuita y astrónomo Ch, Clavius (1537-1612), formuló el Quinto Postulado basándose en equidistancia de la siguiente forma:
Si tres puntos están a un mismo lado de una recta y equidistan de ella, los tres puntos pertenecen a una misma recta
El matemático bizantino neoplatónico Proclo (410-485), en su obra Comentario al libro I de los Elementos de Euclides, tomó como punto de partida una proposición que él atribuyó a Aristóteles (384-322 a. de C.) que dice que las rectas no equidistantes convergen en una dirección y divergen en otra y, a partir de ella, formuló una nueva del Quinto Postulado:
Si una recta encuentra a una de dos paralelas encuentra a la otra necesariamente.
El el matemático inglés J. Playfair (1748-1818) enunció la expresión más popular del Quinto Postulado y, seguramente, fue el culpable de que se le denominara Postulado de las Paralelas.
Por un punto exterior a una recta se puede trazar una recta paralela y sólo una a dicha recta
La mayor parte de las expresiones del Quinto Postulado incluían la idea de paralelismo de una u otra forma y parecían siempre conclusiones evidentes que se explicaban con una representación gráfica, pero en el siglo XVII el matemático inglés J. Wallis (1616-1703) demostró que el Quinto Postulado era equivalente a que en esa Geometría se pudieran construir triángulos semejantes a uno dado de cualquier tamaño.
En realidad la noción de semejanza estaba recogida en el Tercer Postulado, ya que como con cualquier centro y cualquier radio se podía dibujar una circunferencia y, como los triángulos son inscriptibles en una circunferencia, y éstas pueden tener cualquier tamaño (Postulado 3), se puede concluir que existen triángulos semejantes de cualquier tamaño. Pero J. Wallis demostró esa propiedad era equivalente al Quinto Postulado. La demostración la realizó por doble implicación:
En primer lugar: Observó que si se cumplía el Postulado de las Paralelas, evidentemente, debían existir triángulos semejantes de cualquier tamaño.
Luego probó la otra implicación: Demostrando que si se podían construir triángulos semejantes de cualquier tamaño, entonces se debía cumplir el postulado de la paralelas y procedió así:
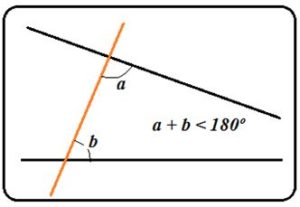
Sean dos rectas AB y CD cortadas por la recta AH y supongamos que los ángulos internos a y b verifican que su suma es menor de dos rectos, es decir: a + b < 180º, veamos que, si se pueden construir triángulos semejantes de cualquier tamaño, entonces se cumple el Postulado de las Paralelas ya que las rectas se cortarán por el lado que verifica a + b < 180º.
Desplazando paralelamente la recta AB hasta la posición CB’’, como por la suposición se cumple que a < 180º- b
La recta AB’’ caerá dentro del ángulo DCH por consiguiente, durante la traslación paralela, la recta habrá pasado por un punto A’ de la recta AH en el que la recta A’B’ habrá cortado a la recta CD. Si P es el punto de intersección de A’B’ con CD, entonces A’H, A’B’ y CD forman el triángulo A’CP. Como por hipótesis se pueden construir triángulos semejantes de cualquier tamaño, en particular existirá uno de delimitado por las retas AH, CD y AB, cuyo vértice será P’, punto de intersección de las rectas AB y CD. Por tanto, las rectas AB y CD se cortan por ese lado, en el que a + b < 180º, por lo tanto, se cumple el Postulado de las Paralelas.
Destacamos la importancia del razonamiento de Wallis que demuestra la equivalencia del Quinto Postulado y la existencia de triángulos semejantes de cualquier tamaño. La prueba de Wallis es cuestionable desde el punto de vista lógico, adolece de lo que Aristóteles denominó petición de principio o razonamiento circular cuando dice en los Primeros Analíticos:
… en efecto, resulta que los que razonan así demuestra A a través de si mismo. Lo cual es precisamente lo que hacen los que creen dibujar paralelas: En efecto, no se dan cuenta que toman cosas tales que no es posible demostrarlas si no existen ya las paralelas. Los que razonan así dicen que cada cosa existe si existe cada cosa: así todo sería conocido por si mismo, lo cual es imposible”[1]
Con lo que se observa que Aristóteles ya cuestionaba, de alguna forma, la existencia de real de rectas paralelas y las demostraciones con ellas en Geometría.
Acomienzos del siglo XIX, C. F. Gauss (1777-1855) obtuvo la siguiente forma equivalente del Quinto Postulado :
Existen triángulos de área tan grande como se quiera.
Todo esto hacía pensar que no aceptar el Quinto Postulado nos transportaba a unos espacios en los que sucedían cosas extrañas. Podía haber paralelas que no se cortaran, podía haber infinitas rectas paralelas a una dada o ninguna y nos llevaba a un espacio en el que no se podían construir triángulos grandes, ni tampoco dibujar figuras semejantes a otra dada de cualquier tamaño. Es decir, no aceptar el Quinto Postulado llevaba a un espacio en el que nuestras intuiciones no se verificaban.
Todos estos trabajos llevaron al convencimiento de que el Postulado de las Paralelas era un verdadero postulado, en el sentido de que era necesario por ser independiente de los otros cuatro. Lo que hizo que surgiera la idea de que aceptar o negar el quinto postulado no debía conducir a contradicciones lógicas, aunque nos transportara a espacios alejados, al menos aparentemente, de nuestras concepciones habituales.
Las investigaciones decisivas sobre los postulados de la Geometría cristalizaron en un momento histórico delicado en el que el filósofo E. Kant (1724-1804) mantenía que el espacio físico era un juicio sintético a priori de nuestra sensibilidad. Como el espacio físico se identificaba con el espacio de la Mecánica de Newton, que se basaba en la Geometría Euclidiana, ésta tenía en aquel momento el marchamo de teoría verdadera y cualquier otra tendría que ser falsa o absurda.
Pero con anterioridad algunos matemáticos, como el jesuita G. Saccheri (1667-1733) habían estudiado el papel del Quinto Postulado en la geometría, analizando si existían contradicciones lógicas aceptándolo o negándolo y descubrieron que no llegaban a contradicciones lógicas. Así parecía que afirmando o negando el Postulado se obtenían teorías coherentes desde el punto de vista lógico y que, a la vez, parecían falsas, porque no se ajustaban a las observaciones en el mundo real. La crisis y el conflicto estaban servidos en el mundo de la geometría.
Estas ideas maduraron a comienzos del siglo XIX y dieron lugar al nacimiento de las Geometrías no Euclidianas con sus protagonistas e iniciadores J. Bolyai (1802 -1860) , N. Lobachevski (1892-1856) y C. F. Gauss que presentaron, geometrías en las que por un punto exterior a una recta se podían trazar infinitas paralelas o ninguna, en las que los ángulos de un triángulo no sumaban 180º, ni existían triángulos semejantes de tamaño arbitrario a otro triángulo dado, ni otras cosas que en la Geometría de Euclides parecían evidentes. Las Geometrías no Euclidianas revolucionaron el mundo de las matemáticas.
[1] Aristóteles, Primeros Analíticos, II; 64b, 65a
