
George Cantor en 1874 había demostrado que el intervalo de los números reales (0, 1) tenía tantos elementos como el conjunto de todos los números reales y más elementos que los números racionales, en realidad, había probado la siguiente relación entre los cardinales de los diferentes conjuntos numéricos:
Card [N] = Card [Z] = Card [Q] = Card [Alg] <
< Car [(0,1)] = Card [R]
Estaba convencido de que existían conjuntos con un cardinal mayor que el del (0,1), cuya infinitud superaba la del continuo, pero tardó en encontrarlos cerca de siete años. Le pareció natural probar si los conjuntos de dimensión mayor que la recta real (dimensión dos, tres, etc) tenían ub cardinal mayor, es decir, demostrar si:
Card [(0,1)x(0,1)] > Card (0,1) = c
Cantor había demostrado de una forma sencilla e intuitiva que los puntos de un intervalo cualquiera de la recta real, en particular (0,1), contenía tantos como la recta R y más que N o Q
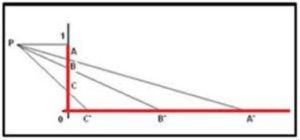
La correspondencia biunívoca entre los puntos del segmento (0,1) (colocado en la ordenada) y la recta R+ se obtiene, simplemente, trazando una recta imaginaria desde un punto auxiliar P (como se observa en la figura), que cortará al segmento (0,1) y a la semirrecta R+ en dos únicos puntos. Se puede observar que a los puntos A, B, C,… de (0,1), les corresponden los puntos A’, B’, C’ de R+.
Lo que demuestra que por cada punto del segmento obtenemos otro que le corresponde sobre la recta, es decir, existe el mismo número de puntos en el segmento que en la semirrecta infinita positiva.
Cantor se planteó el problema de si era posible encontrar un conjunto con un cardinal transfinito superior a c y creyó que la solución estaría en considerar un cuadrado en el plano cartesiano C = (0,1) x (0,1), un cubo en el espacio tridimensional, etc y así sucesivamente. En 1874 escribió una carta a Dedekind en la que le planteaba esta cuestión. Cantor pensaba que no iba a ser posible establecer una biyección entre ese cuadrado y el intervalo (0,1), porque el cuadrado tenía muchos más puntos. Pero, en 1877, descubrió que la correspondencia biyectiva existía y se lo comunicó a Dedekind diciéndole lo veo, pero no lo creo
La correspondencia que encontró fue una que a cada punto P(x,y) de (0,1) x (0,1) le hacía corresponder un punto S del intervalo (0,1) de la siguiente forma:
Si un punto P del cuadrado tenía de coordendas (0,234532781… , 0,8736729382…), S sería el número real 0,283743563722…, es decir, el número que tenía por expresión decimal las cifras intercaladas de la abscisa y la ordenada de P. Cantor había demostrado, que, a pesar de tener el cuadrado dimensión dos y (0,1) dimensión uno, ambos conjuntos tenían el mismo cardinal c.
Si, P(x,y) es un punto del cuadrado (0,1)x(0,1) tal que x = 0,a1 a2 a3 a4 a5… e y = 0,b1 b2 b3 b4 b5… Q, será s= 0,a1 b1 a2 b2 a3 b3 a4 b4… Luego a cada punto del cuadrado le corresponde número real s. Sin embargo, si analizamos la aplicación inversa hay números del intervalo de (0,1) que no tienen su correspondiente en el cuadrado (0,1)x(0,1) por ejemplo a s = 0,102020202… le correspondería el punto (x, y) = (0,122222…;0,000000..) que no pertenece al cuadrado (0,1)x(0,1), ya que tiene la ordenada nula y no pertenece al cuadrado, sino a su frontera.
Lo que Cantor probó era que el cardinal de (0,1)x(0,1) era menor que c, que es el cardinal de (0,1), y como, evidentemente, el cardinal c es menor que el cardinal de (0,1)x(0,1), resulta que tanto (0,1) como (0,1)x(0,1) tienen cardinal c.
No obstante, hay otros conjuntos, que superan la potencia c. Por ejemplo, el conjunto de las funciones reales en (0,1) como se muestra en el siguiente teorema.
Teorema.-El conjunto de las funciones reales en el intervalo (0,1). Tiene una potencia mayor que la del continuo.
Demostración: Sea el intervalo (0,1) que tiene de potencia c y a cada r є(0,1) le hacemos corresponder la función: fr (x) = r/x. (lo que significa que a r = 1/2 le corresponde la función f1/2(x) = 2x a r = 1/4 la función f1/4(x) = 4x) la correspondencia r → fr es inyectiva, de (0,1) en el conjunto de las funciones fr (x) = r/x.
Ahora definimos una función φ(x) tal que para todo r є (0,1)
φ(r) ≠ fr (r)
por ejemplo, que φ(r)= fr (r) +1, φ(s)= fr (s) +1 y así con todos los elementos de (0,1) y, puesto que fr (r) = r/r =1 ⇒ φ(x) = 2 para todo x de (0,1).
Por tanto φ(x), es una finción constante y no pertenece al conjunto de las funciones fr (x) = r/x
En 1891 Cantor logró demostrar que existían cardinales transfinitos mayores que c en sucesivas. Enunciando el Teorema de Cantor que garantiza que existe una cadena de cardinales transfinitos cada vez mayores. El conjunto de las partes de un conjunto A, que designamos con P(A) tiene cardinal mayor que el de A. Este resultado es el teorema de Cantor.
TEOREMA DE CANTOR.- Dado A un conjunto Card [A] < Card [P(A)]




