
Los números naturales son los números que utilizamos para contar u ordenar los elementos de un conjunto. El conjunto de los números naturales es:
N = {0, 1, 2, 3, 4, 5, 6, …}
La primera característica que vamos a destacar de N es la de ser un conjunto ilimitado, de hecho, es el primer conjunto infinito (o transfinito) que procede de una actividad tan sencilla como la de contar. Los conjuntos infinitos tienen una propiedad importante, la que R. Dedekind (1831-1916) utilizó para definir los conjuntos infinitos con la siguiente idea:
Partiendo de la definición de conjuntos equivalentes que eran aquellos entre los que se podía establecer una correspondencia biyectiva. Por ejemplo:
El conjunto A= {1, 2, 3, 4, 5} es equivalente a B = {2, 4, 6, 8, 10} porque a cada elemento de x de A se le puede hacer corresponder el elemento y = 2x de B. Entonces decimos que A y B tienen la misma potencia, la cual está caracterizada por el mismo cardinal: cinco.
Dedekind definió conjunto infinito de la siguiente forma: M es conjunto infinito si existe un subconjunto propio G de M (G C M) equivalente a M. Esta propiedad la tienen los números naturales. Los números naturales tienen la misma potencia (mismo cardinal) que los números pares, ya que N= {1, 2, 3, 4, 5, …} es equivalente a Pares = {2, 4, 6, 8, 10,…}, ya que existe la correspondencia de N en Pares dada por y =2x.
La sorpresa que se produce con la observación de que haya tantos números pares como naturales se repite y amplía con otros conjuntos numéricos que, aparentemente, tienen muchos más elementos que los números naturales.
Un conjunto numérico M tiene tantos elementos como los números naturales, si se puede establecer una correspondencia biyectiva entre M y N . Es decir, si podemos hacer una lista ordenada con todos los elementos del conjunto M.
NUMERABILIDAD DE CONJUNTO Q DE LOS NÚMEROS RACIONALES
El conjunto N de los números naturales está contenido en Q. Parece que hay muchos más números racionales que números naturales. De hecho, entre dos números naturales consecutivos no hay níngún número natural, pero hay infinitos números racionales, por ejemplo, entre 0 y 1 hay infinitos números racionales, la sucesión {1/n}; entre 1 y 2 también infinitos números racionales, la sucesión {(n+1)/n}; lo mismo ocurre entre 2 y 3, etc … .
Sin embargo, hay tantos números racionales como naturales. Podremos probar esta efirmación si podemos escribir los números racionales en una lista, primero, segundo, tercero, etc. Para ello tenemos que establecer una relación de orden en Q y ordenarlos.
La tarea, en principio, no parece fácil, porque no sabemos decir cuál es el número racional que sigue, por ejemplo a 0,5 ¿Es 0,51, 0,501, 0,50001…?. En realidad, no podemos determinar, en el conjunto Q de los número racionales, cuál es el siguiente de un número racional con el orden que manejamos habitualmente, pero si podemos ordenarlos según otro criterio y elaborar una lista que ponga a los número naturales y a los racionales en correspondencia biyectiva.
Teniendo en cuenta que los números racionales son el cociente de dos enteros (denominador no nulo), los podemos ordenar según su Rango. El Rango se define como la suma del numerador más el denominador y las fracciones de igual rango las ordenamos en orden creciente, para conseguir representación univoca. Supondremos que las fracciones son irreducibles (m.c.d (m,n) = 1)
La ordenación según el rango se hace como sigue: Ordenamos los rangos en orden creciente y las fracciones, dentro de las de igual rango en orden creciente:
Rango 1: 0
Rango 2: La fracción 1/1, hay 1
Rango 3: Las fraccones 1/2, 2/1, hay dos
Rango 4: Las fraccones 1/3, 2/2, 3/1 hay tres
Rango 5: Las fraccones 1/4, 2/3, 3/2, 4/1 hay cuatro
Para poner en la lista todos los números racionales (tanto positivos como negativos), detrás de cada número positivo colocamos su opuesto correspondiente:
Q= {0, 1, -1, 1/2, -1/2, 2, -2, 1/3, -1/3, 3, -3, 4, -4, 3/2, -3/2, 1/4, -1/4, …..}
En la que cada número racional tiene su lugar de orden correspondiente.
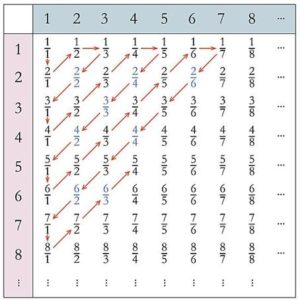
Una forma más gráfica es el procedimiento diagonal. En un cuadrado NxN se eliminan las fracciones que no sean irreducibles y se sigue el camino señalado por las flechas. Cada diagonal se recorre alternativamente en sentido creciente y en sentido decreciente.
NUMERABILIDAD DE CONJUNTO DE LOS NÚMEROS ALGEBRAICOS
Los números algebraicos son las soluciones de las ecuaciones algebraicas, del tipo:
anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0 = 0, donde an, an-1, an-2, … , a1, a0 son números enteros.
Debemos hacer notar que en estos números están incluidos los naturales, los racionales, muchas expresiones radicales buena partes de los números complejos.
Para ordenar los números algebraicos definiremos en primer lugar el Rango de la ecuación que será el número natural:
R = n+|an|+|an-1|+|an-2|+ … +|a1|+|a0 |
Para cada rango hay un número finito de ecuaciones algebraicas y cada ecuación algebraica de grado n tiene, por el Teorema Fundamental del Álgebra n soluciones, que son los números algebraicos asociados a cada ecuación. Para ordenar los números algebraicos procederemos así:
- Ordenamos las ecuaciones según su Rango y si hay ecuaciones con el mismo rango las ordenamos según los sus grados crecientes.
- Las raíces de cada ecuación las ordenamos de menor a mayor. Si son complejas según partes reales crecientes y si las partes reales son iguales según las imaginarias.
Se procede así
R = 1 imposible
R = 2 (Un caso)
Si n=1 y a1 = ± 1 ⇒ a0 = 0 ⇒ ± x = 0 número algebraico 0.
R = 3 (tres casos)
Si n = 1 y a1 = 2, ⇒ a0 = 0 ⇒ ± 2x = 0 número algebraico 0.
Si n = 1 y a1 = ± 1 ⇒ a0 = ± 1 ⇒ ± x ± 1 = 0 números algebraicos 1 y -1.
Si n = 2 y a1 = ± 1 ⇒ a0 = 0 ⇒ ± x = 0 número algebraico 0.
R=4 (seis casos)
Si n = 1 y a1 = ± 1 ⇒ a0 = ± 2 ⇒ ± x ± 2 = 0 números algebraicos 2 y -2.
Si n = 1 y a1 = ± 2 ⇒ a0 = ± 1 ⇒ ± 2x ± 1 = 0 números algebraicos 1/2 y -1/2.
Si n = 2 y a2 = ± 1 ⇒ a0 = ± 1 ⇒ ± x2± 1 = 0 números algebraicos 1, -1, i -i. .
Si n = 2 y a2 = ± 1 ⇒ a1 = ± 1 ⇒ ± x2± x = 0 números algebraicos 0, 1 y -1.
Si n = 2 y a2 = ± 2 ⇒ a1 = a0 = 0 ⇒ ± 2x2 = 0 número algebraico: 0.
Si n = 3 entonces a3 = ± 1 ⇒ a2 = a1 = a0 = 0 ⇒ ± x2 = 0 número algebraico: 0.
Podemos ordenar los números algebraicos:
A= {0, -1, 1, -2, 2, -1/2, 1/2, –i, i,…}



