
Un conjunto H es denso en otro conjunto M cuando el conjunto H está repartido en M de un modo completo. Una imagen intuitiva podía ser el modo de dispersarse el aroma de un perfume por el espacio de una habitación. Alrededor de cada punto de la habitación hay partículas del perfume y el perfume está densamente dispersado.
Los números racionales tiene unas propiedades características:
1.- Entre dos números racionales existen infinitos números racionales
Entre dos números racionales a y b cualesquiera existen infinitos racionales:El punto medio de a y b, los puntos medioa de cada subintervalo y así sucesivamente Podemos seguir indefinidamente, siempre habrá un número racional entre dos, por muy próximos que estén. Se suele decir que Q es denso en R por doquier.
2.- Todavía entre dos números racionales aparecen otros números que no son racionales
En la ecuela Pitagórica se descubrió √2, que está contenido en el intervalo (0,1) , pero no es número racional.
3.- Formamos los números reales R volviendo al continuo, asociando a cada punto de la recta un número. (No tiene las características la concepción filosófica de continuo de Aristóteles, pero es lo que en la ciencia se le llama continuo)
CONJUNTO DENSO. Un conjunto A ⊂ R es denso en R si en cualquier p є R en todo entorno de (p – ε, p + ε) hay algún elemento de A.
Teorema 1. Los números racionales son un subconjunto denso en R
Demostración: p є R, y sea el intervalo (p – ε, p + ε) = (a, b) y veamos que hay un número racional contenido en él. Como b-a > 0 el conjunto N no está acotado (o R es arquimediano), existe n entero tal que :
![]()
Luego en el intervalo (na,nb) hay un número entero m ( la parte entera de na)
Es decir, se cumple que:
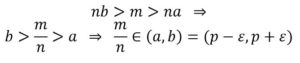
Por lo tanto m/n pertenece al intervalo
Teorema 2 . Los números irracionales, R \ Q, forman un subconjunto denso en R
Demostración:
Sea el intervalo (p – ε, p + ε) = (a, b). Sabemos, por el teorema anterior que hay dos números racionales r y s, tales que a < r < s < b, es fácil comprobar que existe un número irracional
![]()
Que es irracional y que verifica que: a < r < z < s < b
Observación 1: Si los números racionales y los irracionales son densos en R ambos conjuntos están entrelazados sin que podamos separarlos y juntos forman los números reales.
Observación 2 :Los racionales y los números algebraicos siguen siendo numerables. ¿hay más números además de los que los que podemos obtener con las operaciones algebraicas?
Para responder a esta pregunta demostraremos que conjunto de todos los número reales contenidos en el intervalo (0, 1) no es numerable, ya no podremos hacer una lista con todos ellos y si hay más números reales que los que podemos recoger en una lista significará que en (0,1) hay otros números, además de los algebraicos.
Para probarlo Cantor utilizó un métodos que se conoe como Procedimiento Diagonal, que consiste en lo siguiente:
Supongamos que hubiéramos conseguido hacer una lista con todos los números contenidos en (0,1).
1 → 0, a11 a12 a13 a14 a15 ….
2 → 0, a21 a22 a23 a24 a25 ….
3 → 0, a31 a32 a33 a34 a35 ….
4 → 0, a41 a42 a43 a44 a45 ….
Donde los aij son las cifras {0,1,2,3,4,5,6,7,8,9}. A partir de todos estos número podemos formar, además otro número que no está en la lista:
n1= 0, b1 b2 b3 b4…,
donde bi son las cifras {0,1,2,3,4,5,6,7,8,9}. con la condición de que b1 ≠ a11, b2 ≠ a22, b3 ≠ a33, …., bi ≠ aii. Evidentemente, el número n1, es un número del intervalo (0,!) y no está en la lista, quiere decir, que en ninguna lista que podamos hacer, estarán todos los números del intervalo (0,1), por lo tanto (0,1) no es numerable.
Para extender este razonamiento a cualquier intervalo (a, b) basta establecer la relación biunívoca mediante y=a+(b−a)⋅x lo que garantiza la misma numerabilidad que el intervalo (0,1). R tampoco será numerable. R tiene la potencia del continuo.
Así que, teniendo en cuenta que el conjunto de los números reales no es numerable y que los números algebraicos sí lo son, los los números no algebraicos (trascendentes) los que generaban la no numerabilidad. Esto resultaba sorprendente e inquietante en la época de Cantor, ya que sólo se conocían unos pocos números no algebraicos y la mayorúia eran números trascendentes. Los trascendentes eran la materia oscura de los números, eran más abubdantes que los algebraicos, , pero apenas se concocían dos (PI y e), la mayor parte de la matemática se había hecho sin conocer su existencia y Cantor demostró que los números trascendentes existían en abundancia, pero en 1874, apenas se concía alguno.




