
Supongamos que nos enfrentamos a un examen tipo test que consta de 20 preguntas y en el que cada una nos ofrece cuatro alternativas, de las cuales sólo una es verdadera. Por ejemplo:
Pregunta 1. El resultado de la operación 5 x 5 – 5 + 5 x 5 es:
1.- 125 2.- 45 3.- 25 4.- 120
Si esa es la primera de las veinte preguntas del examen, suponemos que todas ellas tienen el mismo valor y si la prueba se evalúa sobre diez, entonces el valor de esa pregunta respondida acertadamente debe tener un valor de 0,5 puntos. Lo que quiere decir que un examen con diez preguntas respondidas acertadamente obtendrá una nota de cinco sobre diez, lo que supone un aprobado justo. Pero no es así, porque un examen tipo test tiene unas características especiales derivadas del hecho de que, una persona respondiendo al azar podría acertar la cuarta parte de las preguntas del examen, es decir, cinco, lo que supondrá que la nota mínima media de los que así respondan será 2,5, lo que parece una injusticia o una ventaja, para los que no saben nada del tema, ya que una persona que conteste correctamente (porque conoce el tema) a siete preguntas aprobará el examen contestando las trece preguntas restantes al azar.
Un examen, del tipo que sea, sirve para evaluar conocimientos o habilidades. Y la calificación del mismo debe diseñarse para que las calificaciones varíen en una escala de cero a un valor máximo que elegiremos como diez. En un examen tradicional la calificación mínima cero puede obtenerse si el examen se deja en blanco o lo que se responde pone de manifiesto un desconocimiento total de la materia. En un examen tipo test existe una probabilidad de aprobar por mero azar, por lo que haremos un análisis probabilístico del mismo.
Vamos a determinar cuál sería la fórmula correcta desde el punto de vista de las probabilidades para puntuar en un examen test, y lo justificaremos desde el punto de vista matemático realizando las siguientes consideraciones. En primer lugar, supondremos que cada pregunta tiene una única respuesta y que todas las preguntas valen lo mismo. Que las preguntas no respondidas ni suman ni restan y que las preguntas falladas restan puntuación. Esta última condición se impone para minimizar la influencia de la suerte para el que elige al azar. Designaremos la penalización a las preguntas falladas con x y la determinaremos
Consideremos las siguientes características que definen un examen tipo test:
Hay n preguntas que puntúan lo mismo; cada una de ellas tiene m respuestas posibles y sólo una de ellas es válida. La puntuación máxima del examen es de n, por lo tanto, cada pregunta acertada debe puntuar un punto. La penalización por error es x.
Es evidente que la penalización por cada pregunta fallada debe estar relacionada con el número respuestas propuestas en cada pregunta.
Queremos proponer un test tal que el que responda todas las preguntas al azar espere sacar un 0. Aunque se pueda dar el caso que en el examen se pueda sacar lo nota máxima e incluso una nota negativa.
Llamaremos c1, c2, … cn a la calificación obtenida en cada una de las preguntas, de forma que la nota total será:
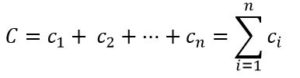
Entendiendo que responder por puro azar significa que todas las respuestas propuestas en cada pregunta tienen idéntica probabilidad de ser elegidas y marcadas, tenemos lo que los matemáticos llaman una distribución uniforme sobre las posibles respuestas.
Si, cada pregunta tiene m posibles respuestas, la probabilidad de acertar al responder de manera aleatoria es 1/m y la probabilidad de fallar es 1-(1/m). Ya tenemos todos los datos para definir la variable aleatoria
ci= calificación obtenida en la pregunta i”

Calculemos ahora la calificación esperada en cada pregunta será la esperanza matemática de la variable aleatoria ci. Esta esperanza se calcula:

Deseamos calcular la penalización x para que la nota esperada cuando se contesta al azar se cero, la penalización por cada fallo debe ser:
![]()
Si ahora tomamos la variable aleatoria:
Y como queremos calcular la nota esperada en el examen, vamos a calcular la esperanza de esta nueva variable aleatoria que la esperanza de la suma es igual a la suma de las esperanzas)

Ejemplo Si una persona realiza un examen tipo test de 90 preguntas con cuatro alternativas y responda a 80 de ellas, cometiendo 9 fallos obtendrá: (con 71 aciertos y 9 errores) utilizando la fórmula (1)

68 sobre 90, aproximadamente un 7,5 sobre 10.




