
El concepto de infinitésimo apuntaba su aparición desde los comienzos de las matemáticas. Con los procesos infinitos se asomó de la mano del descubrimiento de los números irracionales cuando se demostró la inconmensurabilidad del lado y la diagonal del cuadrado. Pero tanto lo infinitamente pequeño (el infinitésimo), como lo infinitamente grande (el infinito) se consideraban como algo que no se podía alcanzar en la realidad; ambos eran resultados de procesos indefinidos. De hecho, se distinguía en infinito actual e infinito potencial.
N. Cuesta Dutari (1907-1989) en su artículo Tres notabilísimos pasajes de Euclides (1981) presenta un ejemplo del infinitésimo actual y es el ángulo keratoideo o corniforme.

El concepto en que se basa es en la medida de una relación: la inclinación de una línea respecto a otra. Debemos tener en cuenta que Euclides define ángulo entre dos líneas, que no tienen necesariamente que ser rectas.
En la Definición 8 del Libro I de los Elementos de Euclides (325-265 a.C.) define ángulo de la siguiente forma:
Angulo plano es la inclinación mutua de dos líneas que se encuentran una a la otra en un plano y no están en línea recta
En la Proposición 16 del Libro III de los Elementos, Euclides proporcionó una visualización del ángulo keratoideo o cero, ángulo entre la circunferencia y una recta tangente en un punto de ella, que dio lugar a futuras reflexiones sobre los infinitésimos
Proposición 16.- Si en el extremo de un diámetro AB se levanta una recta perpendicular AD, ésta cae fuera del círculo y entre la recta y la circunferencia no se puede interponer ninguna otra recta.
En la figura observa que entre la circunferencia ACB y su tangente AC, cualquier recta AX cortará a circunferencia y, por lo tanto, no está interpuesta entre la circunferencia y la recta AB. Es decir, ninguna recta estará interpuesta entre la circunferencia y la tangente AB (dentro del ángulo).
El concepto de ángulo corniforme fue retomado por I. Newton (1642-1727) como justificación geométrica del uso de cantidades evanescentes y de distintos niveles de cero o, lo que es igual diferentes órdenes de infinitésimo. Así, Philosophiae Naturalis Principia Mathematiea (1687), después de las definiciones preliminares de masa, cantidad de movimiento, fuerza de inercia, fuerza impresa, centrípeta y exponer las leyes del movimiento (ley de inercia, ley del cambio de movimiento y ley de acción y reacción). En la sección primera del Libro I de los Principia, exponía las Primeras y Últimas Razones de Cantidades. Las cuales son el soporte matemático de la obra y la parte predominante de una formulación geométrica del estudio de movimiento en la obra.
No obstante, para justificar sus razonamientos y, quizás futuros acercamientos desde el Álgebra y la Geometría Analítica al estudio del movimiento. En el Escolio final de la sección primera plantea que hay distintos niveles de ángulos corniformes, lo que significa diferentes grados de cero y, en suma, diferentes tipos de infinitésimos.
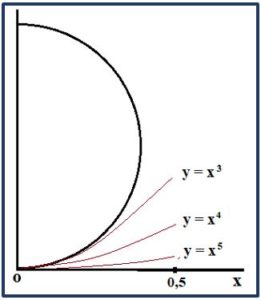
Aunque el dibujo no guarda escala, podemos decir que así como en la región comprendida entre la circunferencia y la recta tangente cabe ningún ángulo rectilíneo tal que uno de sus lados sea la tangente, si caben ángulos formados por la tangente (eje OX) y la circunferencia.
Se puede comprobar simplemente dando valores en un entorno suficientemente pequeño del origen 0, que entre la recta tangente caben los ángulos corniformes que forma el eje OX con las curvas y = x3, y = x4, y = x5,… que son ángulos menores que el ángulo corniforme de medida cero que forman a circunferencia y la tangente. En suma, son ceros (infinitésimos) más pequeños de orden superior.
Tomando La circunferencia x2 + (y-1)2 = 1 ⇒ y = 1-√(1-x2) se observa en la siguiente tabla que y = x4, y = x5 … son progresivamente infinitésimos de orden superior, a partir de x2, ya que entran dentro del ángulo corniforme de la ciecunferencia,





