
La Fisica Griega, representada por las tesis de Aristóteles (384-322 a.C.), no admitía la existencia del vacío. Mantenía que la naturaleza se resistía a tolerar la ausencia de aire, no se concebía un espacio sin materia y la Física de Aristóteles hizo del horror vacui un principio absoluto. En el Libro IV de su Física expuso los principales argumentos a favor y en contra de la existencia del vacío y desmontó las tesis principales de los filósofos que defendían su existencia, sobre todolas de pensadores procedentes mayoritariamente de la Escuela Atomista de Leucipo y de Demócrito.
La mayor parte de las escuelas filosóficas de la antigüedad negaban la existencia del vacío y esta idea filosófica se mantuvo como una premisa física y como una convicción profunda del pensamiento a lo largo de la Edad Media y sólo se llegó a cuestionar a mediados del siglo XVII.
Desde la religión se argumentaba que el vacío no podía existir. Los escolásticos argumentaban que el vacío no podía producirse en la Naturaleza con silogismos como e siguiente: Dado que Dios no puede actuar en la nada, como el vacío es igual a la nada y Dios es omnipresente, el vacío no podría existir. Un argumento en el que se aludía a la intervención divina para generar el vacío era el de R. Descartes (1596-1650): Si Dios, por un milagro, retirara toda la materia de un recipiente e impidiera que otra materia ocupara su lugar, entonces las paredes del recipiente se juntarían, dado que una extensión no puede existir sin sustancia
El horror vacui permitía interpretar fenómenos como el llenado de líquido de una jeringuilla, la absorción de un refresco con una paja o la dificultad para separar un fuelle cuando se impedía la entrada del aire. Todas estas situaciones podían explicarse por la tendencia de la naturaleza a no dejar espacios vacíos. La naturaleza no soportaba la ausencia de aire. Hoy sabemos que cuando, por jemplo, tomamos un refresco con una paja, el líquido llega a nuestra boca por la presión que ejerce el aire circundante, sobre la superficie del líquido del vaso, pero en la Edad Media se interpretaría suponiendo que el líquido tendía a llenar el vacío que creamos en la paja al absorber y la experiencia no haría otra cosa que reforzar algo que ya se sabía mediante un principio filosófico general: La naturaleza tiene horror a vacío.
GALILEO Y LA MEDIDA DEL VACÍO
Galilei (1564-1642) mantuvo la creencia heredada de que la naturaleza tenía horror al vacío y la dejó plasmada en su obra Consideraciones y demostraciones matemáticas sobre dos nuevas ciencias (1638), donde describió como funcionaba una bomba aspirante para sacar el agua de una cisterna y sus limitaciones para elevar el agua a cualquier altura. Al principio, dice Galileo, la bomba lanza agua abundante, pero a medida que el nivel del agua de la cisterna desciende la bomba extrae menos agua y, finalmente, llega un momento en el que la bomba deja de actuar.
Galileo había inventado en 1593 una bomba aspirante para elevar agua. Y la instaló en 1604 para regar los jardines de la casa Contarini de Padua. La bomba funcionaba correctamente, pero pronto recibió una carta de Contarini en la que le decía que la bomba no podía elevar agua por encima de 10 m. Galileo le contestó que se debía a que del mismo modo que para vencer la fuerza vacío que se creaba entre dos láminas planas hacía falta otra fuerza, el horror al vacío en la naturaleza implicaba dificultad y, aunque no era un obstaculo invencible y se podría superar con la fuerza suficiente, la bomba no poseía esa fuerza.
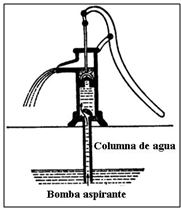
Galileo dio también una interpretación mecánica de funcionamiento de la bomba, sin tener en cuenta para nada la presión atmosférica. Pensó que si las bombas no podían subir el agua por encima de cierta altura se debía a la naturaleza del agua y dio una ingeniosa argumentación basada en el horror al vacío de la Naturaleza. Pensó que, del mismo modo que una cuerda colgada cada vez más larga acabaría rompiéndose por su propio peso, la columna de agua que subía por el tubo de la bomba debía acabar rompiéndose por su propio peso y diez metros era la máxima longitud que podía alcanzar el cilindro de agua. El peso del agua contenida un tubo de diez metros medía la resistencia de la fuerza del vacío en los cilindros de agua. Galileo utilizó esta idea para medir el horror vacui de diferentes materiales existentes en la naturaleza y calculó las longitudes máximas que podían alcanzar hilos de diferentes materiales sin romperse por su propio peso.
E. Torricelli (1608-1647) fue un físico y matemático italiano, discípulo de B. Castelli (1577-1643), amigo de Galileo y profesor de la Universidad Pisa. En 1641, Galileo, ya anciano en su arresto domiciliario de Arcetri y ciego, tomó como ayudante, por recomendación se Castelli, a Torricelli que se convirtió en ayudante, amanuense y discípulo de Galileo hasta la muerte de pisano en enero de 1642. Y fue precisamente este genial discípulo el que dio una interpretación muy diferente del funcionamiento de la bomba aspirante de Galileo.
Torricelli conocía bien la obra de Galileo y, en particular, Consideraciones y demostraciones matemáticas y sabía la explicación que había dado Galileo al problema imposibilidad de elevar agua por encima de los diez metros con una bomba aspirante. Sin embargo demostró que el agua de la cisterna no subía más porque la presión que ejercía la columna de agua sobre la superficie del agua debía ser igual a la presión atmosférica que se ejercía sobre la superficie del agua de la cisterna sin suponer la suposición no probada de que la naturaleza tuviera resistencia al vacío.

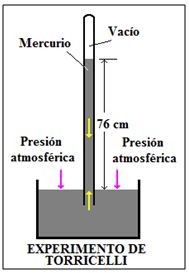
Torricelli llevó a cabo en 1644 un experimento, pero utilizando mercurio, que tiene una densidad 13,6 g/cm3 en lugar de agua. Llenó de mercurio un tubo de, aproximadamente, un metro de largo e introdujo el extremo abierto en una cubeta de mercurio. El mercurio comenzó a salir del tubo por el extremo abierto, pero cuando alcanzó una altura de unos 760 mm sobre el nivel de la cubeta dejó de salir y permaneció al mismo nivel. Repitió el experimento con tubos de diferentes secciones y alturas y formas y obtuvo el mismo resultado. El experimento de Torricelli no solo permitió medir la presión atmosférica, sino que, además, creó el vacío en la parte superior del tubo. Era la primera vez que se obtenía el vacío en un experimento.
Torricelli aventuró la idea revolucionaria, que rompía con la creencia aristotélica de que el aire, que era uno de los cuatro elementos de la Física Griega (Tierra, Agua, Aire y Fuego), no tenía peso, ya era ingrávido, porque sólo tenía movimiento ascendente. Torricelli interpretó el experimento en el siguiente sentido: la columna de agua de diez metros de altura y la de 76 cm de mercurio medían el peso de la atmósfera, es decir, medían el peso de una columna de aire del mismo diámetro con una altura desde el nivel del mar a la parte más alta de la atmósfera. Observó que una columna de mercurio de 76 cm de alto ejercía la misma presión que una columna de agua de 10 metros (aproximadamente). Para calcular la altura de que alcanzaría el agua de la bomba aspirante de Galileo con mayor exactitud realizó el siguiente cálculo:
Una altura h de agua ejerce una presión
p1 = (1 g/cm3)· (980 cm/s2)·h
Una altura de 76 cm de mercurio ejerce una presión:
p2 = (13,6 g/cm3)· (980 cm/s2)·76 cm
Para que las presiones sean iguales p1 = p2 de donde:
h = 13,6 ·76 ⇒ h = 1034 cm = 10,34 m
que en la altura de agua que marcaba la limitación de la bomba aspirante.,
El experimento de la bomba aspirante fue analizado por Galileo y Torricelli de dos formas distintas. Galileo explicaba el hecho de que las bombas aspirantes no pudieran elevar agua por encima de los diez metros porque la naturaleza se resistía al vacío y esos metros medían la resistencia de la naturaleza a crearlo. Mientras que Torricelli consideraba que el peso de la columna de agua sólo equilibraba el peso de la atmósfera. Tras el experimento de Torricelli con el barómetro de mercurio había más indicios de certeza en las tesis de Torricelli, puesto que, el peso de una columna de agua de diez metros y treinta y cuatro centímetros era el mismo que el de una columna de mercurio de 76 cm. Pero ¿Quién había sentido el peso de la atmósfera?. Si la atmósfera ejercía una presión próxima a un kilogramo por centímetro cuadrado, el peso del aire sobre un hombre debía ser unos quinientos kilogramos y nuestros sentidos no lo apreciaban se apreciaba por los sentidos.
B. Pascal (1623-1662) realizó una prueba concluyente a favor de las tesis de Torricelli demostrando que el aire pesaba. Las contribuciones de Pascal al estudio de los líquidos y de los fluidos fueron numerosas. Se le considera el inventor de la prensa hidráulica y de la jeringuilla. Sus aportaciones al tema contribuyeron a precisar el concepto de presión en los fluidos, de hecho, la unidad de medida de la presión se llama Pascal.

El experimento crucial para decidir entre las explicaciones dadas por Galileo y Torricelli lo realizó en 1647. Pascal pensaba que, si la atmósfera tenía peso, tal y como pensaba Torricelli y tenía un espesor, a medida que nos fuéramos elevando el grosor de la capa de aire que tendremos sobre nosotros será menor y el peso de la misma y, por tanto, la presión también será menor. Pascal le encargó a su cuñado Perier, que vivía en Clermont Ferrand, que subiera al Puy-de-Dôme y midiera con un barómetro de Torricelli la disminución de la altura de la columna de mercurio o, lo que es igual la disminución de la presión con la altura desde el valle donde vivía hasta la cima del monte. Périer obtuvo el resultado, para un desnivel de 984m, una disminución en la columna de mercurio de 8’50 cm. Lo que demostraba que la presión atmosférica disminuía a medida que aumentaba la altura. El experimento del Puy-de-Dôme corroboró la hipótesis Torricelli y refutó las tesis mecánicas de Galileo.




