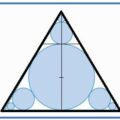
Cuando hablamos del centro de un círculo no tenemos ninguna duda, el centro de un círculo es un punto interior del mismo que se encuentra a la misma distancia de cualquier punto de su periferia (circunferencia), pero, si queremos referirnos al centro de un triángulo, ¿Qué punto debemos tomar como centro?.
Nos parecerá lógico tomar como centro del triángulo el punto que equidista de los vértices del triángulo, llamado circuncentro, y que es el centro de la circunferencia circunscrita al triángulo, pero nos parecerá igualmente lógico, tomar como centro el punto que equidista de sus lados, llamado incentro, que sería el centro de la circunferencia inscrita. Y puestos a fijarnos en las distancias ¿Por qué no elegir como centro del triángulo el punto de Fermat del mismo que cumple la condición de que la suma de distancias a los tres vértices es mínima?
Si ampliamos el aspecto geométrico de la pura distancia y consideramos el triángulo como un cuerpo material, con peso y con distribución homogénea de masa, aparece el concepto de centro de gravedad, centroide o baricentro, cuya noción puede resumirse diciendo que los objetos sometidos a la gravedad se comportan como si existiera una sola fuerza aplicada en él. Si un cuerpo, en este caso el triángulo, está apoyado en su centro de gravedad se mantendrá estable y no tenderá a moverse, a inclinarse ni a girar en ningún sentido.
Propiedades el centro de masas de un triángulo a partir del c d g de dos masas puntuales: m1 situado en x1 y m2, situado en x2 será un punto x0 situado entre x1 y x2, tal que:
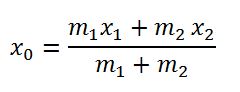
En una superficie plana homogénea de dos masas puntuales: m1 y m2, situadas en los puntos A (x1, y1) y B(x2, y2)
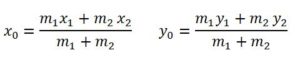
Una varilla homogénea, tendrá su centro de gravedad en el punto medio.
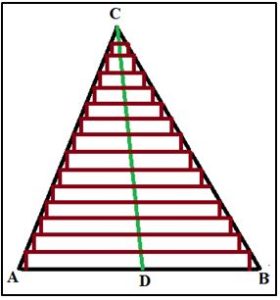
Una forma intuitiva de determinar el centro de gravedad de un triángulo de cartulina (con distribución homogénea de masa en toda su superficie) se puede hacer descomponiendo el triángulo en tiras muy estrechas paralelas al lado AB. El centro de gravedad de cada tira estará en su punto medio, y resultara que el c. de g. del triángulo se encontrará en la mediana del triángulo trazada desde el vértice C al lado AB. Y, como él mismo razonamiento, puede aplicarse descomponiendo el triángulo en tiras paralelas a los otros dos lados resulta que el triángulo tiene su centro de gravedad en el punto de intersección de las medianas (que intuimos, que se deben cortar en un punto).
En geometría existe un teorema importante para saber si tres rectas trazadas desde los vértices de un triángulo se cortan en un punto. Es el teorema del matemático Italiano G. Ceva (1647 -1734), que dice lo siguiente:
TEOREMA DE CEVA.- Si desde los vértices A, B y C de un triángulo se trazan tres rectas que determinan con los lados opuestos tres puntos N P y M respetivamente que cumplen que:
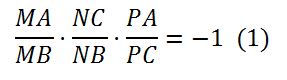
Las rectas se cortan en un punto G
El teorema se puede aplicar para demostrar que las tres medianas de un triángulo tienen un punto común. Si las rectas son las tres medianas, entonces M es el punto medio de AB, N es el punto medio de BC y P el punto medio de AC, por tanto, se cumple que:
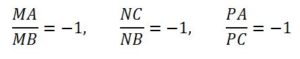
y se verifica:
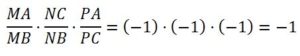
y las tres rectas (Por el teorema de Ceva) tienen un punto común, G, que será el baricentro.
Que las tres medianas tiene un se puede demostrar desde la geometría elemental usando los conceptos semejanza y la paralela media de un triángulo.
TEOREMA 1.- Las medianas se cortan en un punto G tal que:
AG =2AN/3 BG= 2BP/3 y CG= 2CM/3
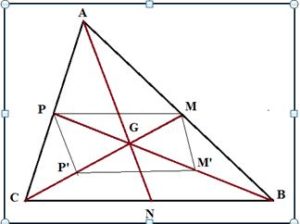
Demostración:
Las medianas CM Y BP se cortan en un punto G. Tomemos, sobre la mediana CM, el segmento GP’ = GM y, sobre la media mediana BP, GM’ = GP.
Entonces PM es la paralela media del triángulo ABC correspondiente al lado CB y mide la mitad de C B.
Igualmente P’M’ es la paralela media de CB en el triángulo GBC y mide la mitad de CB, por lo tanto PMM’P’ es un paralelogramo y el punto G es donde se cortan las diagonales, por lo tanto, GP’= GM = CP’, de dónde se sigue la tesis
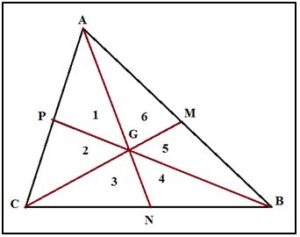TEOREMA 2.- las medianas de un triángulos de área A lo dividen en seis triángulos iguales de área A /6.
Es evidente que Area (3) = Area (4), ya que las bases de los triángulos CNG y NBC cumplen que sus bases CN = NB y tienen la misma altura. Por la misma razón:
Area (1) = Area (2) y Area (5) = Area (6)
Como los triángulos ANC = 1 + 2+ 3 y ANB = 4 + 5 + 6, tiene la misma área
Area (1) + Area (2) + Area (3) = Area (4) + Area (5) + Area (6 ) (1) ⇒
2·Area (1) + Area (3) = Area (4) + 2· Area (6 ) como Area (3) = Area (4)
Area (1) = Area (6)
Partiendo de que Área de ABP = Área de BPC se llega a que Área (4) = Área (5) con lo que se completa la demostración,
