A comienzos de la década de 1920 el biólogo italiano Humberto D’Ancona (1896-1964) observó la evolución de las poblaciones de varias especies de peces que interactuaban entre sí. Disponía de datos de las capturas que entraban en algunos puertos del mar Adriático (Fiume, Venecia y Trieste) durante los años de la Primera Guerra Mundial (1914-1918) y siguientes.
D’Ancona observó que durante ese periodo había aumentado el porcentaje capturas de seláceos (tiburones, tintoreras y rayas) y concluyó que el incremento del porcentaje de seláceos se debía a la disminución de la actividad pesquera durante el periodo bélico. Como la pesca de peces para consumo humano había disminuido por la guerra habría tenido que aumentar (si vivieran solos en el mar), pero ese supuesto aumento no se produjo, en realidad había menos porcentaje de peces pequeños (sardinas, caballas, doradas jureles etc.) ya que eran el alimento de los peces predadores, y la población de depredadores, cuanto más alimento tenía más aumentaba y había más consumo de peces pequeños.
En 1926 D’Ancona se casó con Luisa Volterra, hija del matemático Vito Volterra (1860-1940) y el relato de D’Ancona a su suegro de sus observaciones sobre la influencia la reducción de la actividad pesquera en el evolución de las poblaciones de peces inspiró el trabajo de Volterra sobre biología matemática.
Volterra estableció un sistema de ecuaciones logísticas para describir el crecimiento de poblaciones competitivas y con ellas estudió cómo afectaba la reducción de la actividad pesquera en las variaciones de la población de los peces pequeños y de sus depredadores.

Alfred J. Lotka (1880-1949), químico y matemático norteamericano de origen ucraniano, que estudió en Leipzig con el Premio Nobel de Química de 1909 F. W. Ostwald (1853-1932) y trabajó con la ecuación logística de P.F. Verhulst (1804-1859), con el fin de describir el intercambio de energía en una reacción química en la cual las concentraciones oscilaban. Inspirado, seguramente, en los procesos de las reacciones químicas publicó en 1925 el libro Elementos de Biología Física, que es el primer libro escrito de biología matemática (el libro fue reeditado después de la muerte de su autor con el título: Biología Matemática). Lotka publicó el modelo que hoy se conoce como modelo Lotka-Volterra y que representa, aún en la actualidad, la base de los estudios teóricos sobre la dinámica de poblaciones. Lotka acuñó una nueva terminología y definió conceptos como población estable, población estacionaria o tasa de crecimiento natural. A A. Lotka y a V. Volterra se les considera los fundadores de la demografía matemática.
El modelo matemático Lotka-Volterra expresa en forma matematica la interdependencia entre las especies con la relación presa-predador. El modelo se plantea a partir de la base observacional que hemos esbozado. Es decir, las ecuaciones reflejan lo siguiente: si hay muchos predadores el número de presas descenderá y ese descenso de presas provocará que haya menos predadores que se puedan alimentar y la población de predadores acabaría descendiendo. Por otra parte, si no hubiera predadores las presas crecerían exponencialmente sin otra limitación que la capacidad del hábitat en que se desenvuelvan. Si no hubiera presas los predadores desaparecerían con un decrecimiento exponencial negativo
Para elaborar el modelo consideraremos que la especie depredadora se alimenta solo de presas de una sola especie, mientras la presa encuentra en su hábitat recursos ilimitados de alimentación, predecir la evolución global cualitativamente es sencillo, lo que resulta algo más complejo es saber que ocurrirá en una situación de cuasi-equilibrio, en la que se pueden ver situaciones como las oscilaciones del sistema o la aparición de un cierto patrón oscilatorio común: atractor de ciclo límite.
El sistema de ecuaciones se plantea de la siguiente forma:
Sea x(t) es el número de presas e y(t) el número de predadores en un instante t. Planteemos las ecuaciones:
Primera ecuación: Si no hubiera predadores, las presas crecerían de acuerdo con la ley de crecimiento exponencial x′(t) = αx(t) y, si suponemos que el número de muertes de presas por unidad de tiempo es proporcional al número de encuentros presa-depredador, el número de muertes será: βx(t)y(t). Por lo tanto, la ecuación será:
x′(t) = αx(t) – βx(t)y(t) ⇒ x′(t) = x(t) (α – β y(t)
Segunda ecuación: Los depredadores tienen una tasa de mortalidad a una razón de y′(t) = – 𝛾y(t) para alguna constante positiva 𝛾. Parece razonable suponer que están prosperando y creciendo (ya que se están alimentando) a una razón δ·x(t)y(t) proporcional al número de predadores en ese momento y(t) y al suministro de alimento (presas) x(t).
y′(t) = – 𝛾 y(t) + δ·x(t)y(t) ⇒ y′(t) = – y(t)( 𝛾 – δ·x(t))
Por tanto el sistema será:
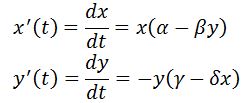
Donde α, β, γ y δ son parámetros que representan las tasas de crecimiento o decrecimiento y de interacción entre las dos especies:
- α representa la tasa de crecimiento de las presas (o tasa de natalidad de las presas),
- β representa la tasa de eliminación de las presas por parte de los predadores (o la tasa de eficiencia de captura),
- γ representa la tasa de eliminación natural de los predadores (o tasa de mortalidad de los predadores)
- δ representa la tasa de crecimiento de los predadores como resultado del consumo de presas (o tasa de transferencia energética de las presas a los predadores).
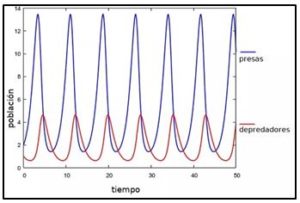
Si los parámetros γ y δ son distintos de cero el sistema es de segundo orden, con retroalimentación, en el que los resultados de la primera ecuación intervienen en la segunda y recíprocamente. En este caso, el sistema de ecuaciones diferenciales no se puede resolver analíticamente en términos de funciones elementales. Se pueden utilizar métodos numéricos, como el de Euler o Método de Runge-Kutta. y se obtienen representaciones de las soluciones como la siguiente, en la que se observa que el cambio periódico en la población de presas se corresponde con un cambio, también periódico en la población de depredadores, pero las variaciones van desfasadas. También se observa que el tamaño de las poblaciones oscila dentro de un intervalo de valores, es decir, que predadores y presas mantienen un equilibrio dinámico, lo que significa que lo que afecta a las presas repercute en los predadores a largo plazo, y que una variación en la población de cualquiera de las dos especies afecta a la otra.
Del sistema de ecuaciones se deduce inmediatamente que las poblaciones tienen unos puntos fijos, llamados puntos de equilibrio en los que las poblaciones de ambas especies permanecen invariables, lo que significa que en esos puntos se cumple que :
x’(t) = 0 e y’(t) = 0 ⇒ 0 = x (α – β y) e 0 = y (𝛾 – δx)
De donde obtenemos los dos puntos de equilibrio A = (0,0) y B = (α/β, γ/δ). El punto A no nos interesa porque x = 0, e y = 0, lo que significa que las poblaciones se han extinguido, tiene interés el punto B en el que x = α/β e y = γ/δ.
A continuación damos de forma esquemática una aproximación analítica del comportamiento periódico de las poblaciones de predadores y presas entorno al punto de equilibrio B:
Sean X e Y las desviaciones de las poblaciones x e y respecto al punto de equilibrio, por tanto:
x = α/β + X e y = γ/δ + Y
Sustituyendo en el sistema x’ = x (α – β y) e y‘ = y (𝛾 – δ·x) se obtiene:
x’(t) = (α/β + X) (α-β (γ/δ + Y)) y’(t) = – ( γ/δ + Y) (γ- δ (α/β + X))
Operando resulta:
X’(t) = (𝛾β/𝛿) X+ βXY Y’(t) = – (α𝛿/β) Y– 𝛿 X Y
Podemos obtener una aproximación linealizando el sistema anterior y queda::
X’(t) = (𝛾β/𝛿) X Y’(t) = – (α𝛿/β) Y
Dividiendo miembro a miembro:
Y’(t)/ X’(t) = – (𝛾β2/α𝛿2)) X/Y ⇒ Y(t)·Y’(t) = – (𝛾β2/α𝛿2)) X(t)·X’(t)
Integrando y arreglando constantes de integración queda:
𝛾β2 X2 + 𝛿2α Y2 = C2.
Que es una familia de elipses que rodea al origen del plano XY, que se corresponde con una familia de curvas como se indica en la gráfica siguiente:

Aunque modelo Lotka-Volterra es de gran utilidad en el estudio de la evolución de poblaciones, en la naturaleza, los fenómenos de extinción de especies o el comportamiento cíclico alrededor del punto fijo no se observan de manera tan clara, ya que los depredadores tienen más de una presa de que alimentarse. Cuando un tipo de presa abunda es fácil cazarla y su población desciende, pero si hay más presas el depredador puede cazar otras especies, y la primera especie inicial puede recuperar el número de individuos de equilibrio.