Desde la antigüedad se sabe que la longitud de la circunferencia es un poco más que tres veces su diámetro y que con cada vuelta completa de una rueda, se recorre una distancia igual a la longitud de la circunferencia que forma la rueda. Esta propiedad se ha empleado en la práctica para medir la longitud de la circunferencia, que en geometría. se llama rectificación de la circunferencia porque se trata de determinar un segmento rectilíneo que mida lo mismo que la circunferencia.
El procedimiento geométrico más intuitivo para rectificar circunferencia es por rodadura. Consiste en hacer una marca en un punto O de la circunferencia, hacerla rodar sin deslizamiento siguiendo una línea recta y medir sobre ella la distancia OO’ entre las dos veces consecutivas en las que el punto O toca la recta’. Tal como se muestra en la figura siguiente:

Este método físico, tan claro e intuitivo, de rectificación de la circunferencia ha llevado a paradojas aparentes debido a que se olvida la premisa de que la rueda debe rodar sin deslizamiento
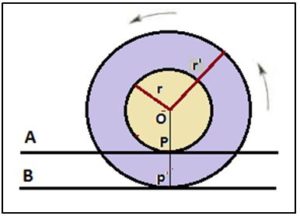
Es la paradoja que parece presentarse cuando se considera el movimiento de dos ruedas concéntricas solidarias como las que se presentan en la figura. Ruedas del tren o ruedas con centro de giro común que giran unidas. El disco pequeño de radio r rueda sin deslizamiento por la recta horizontal A y el grande de radio r lo acompaña en su movimiento solidario por la B. Cuando en su avance hacia la izquierda y los puntos P y P’ estén de nuevo en vertical, podríamos concluir que las circunferencias de los dos discos tienen la misma longitud, pero, evidentemente no es así, porque la rueda pequeña sólo gira y la grande gira y se desliza. En realidad debemos pensar cuál será la trayectoria de los puntos P y P’ en ese movimiento. Está claro que no describen una línea recta. El punto P describe una curva que se llama cicloide, como se muestra en la figura.
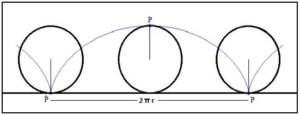
La cicloide es la curva plana que describe un punto de una circunferencia que rueda sin deslizarse sobre una recta horizontal.
En el caso de la rueda de un tren en la que la rueda pequeña rueda sobre el raíl y la grande es solidaria los puntos de las mismas describe trayectorias como las siguientes: La rueda pequeña describe una cicloide normal y la grande una cicloide alargada, e longitudes diferentes, como se indica en la figura:
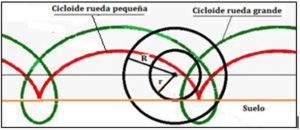
La cicloide fue llamada la Helena de la geometría en recuerdo a la mujer de Menelao, de quien se decía que por ella se lanzaron al mar un millar de barcos. Igualmente, la cicloide, con sus innumerables propiedades geométricas y físicas despertó e interés de muchos matemáticos e incluso fue motivo de disputas entre algunos de ellos. Como el litigio por plagio que se produjo entre E. Torricelli (1608-1647) y G. Roberval (1602-1675).
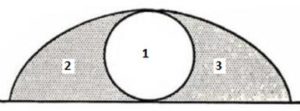
El primero demostró en 1643 que el área encerrada entre un arco de la curva y la línea de rodadura era tres veces el área del círculo que la generaba y hoy se sabe que Roberval había demostrado hacia 1632 el mismo resultado por el método de los indivisibles de B. Cavalieri (1591-1647), aunque no se publicó hasta 1693. Esta es fue la primera propiedad geométrica importante de la cicloide: que el área bajo la curva era el triple el área del círculo,. En la figura que las áreas señaladas con 1, 2 y 3 son iguales.
Otra propiedad geométrica importante fue obtenida por Christopher Wren (1632-1723) que demostró que la longitud de un arco de cicloide era ocho veces el radio de la circunferencia que la generaba.
La curva tenía dos propiedades físicas importantes. La primera es propiedad braquistócrona (del griego brachistos “el más corto” y chronos “tiempo”) Esto significa que la cicloide es el camino más rápido que puede seguir una partícula entre dos puntos A y B (que no estén en vertical ni en horizontal) partiendo de una velocidad nula y sometida solamente a la fuerza de la gravedad. En suma, la cicloide era la forma de un tobogán por el que podía descender una partícula de A a B en tiempo mínimo.
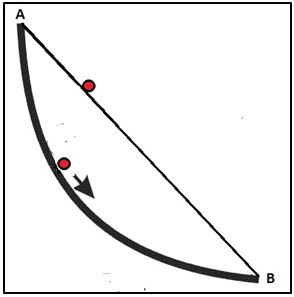
Se sabe que el camino más corto entre dos puntos A y B, es el segmento de línea recta que los une. Pero el tiempo que emplea una partícula para ir de A a B no depende solamente de la longitud del camino. sino que es función, además, de la velocidad de la partícula.
La historia de esta propiedad es curiosa y estuvieron involucrados los dos padres del cálculo infinitesimal, I. Newton (1643.1727) y G. Leibniz (1646-1716). En 1696 el matemático suizo J. Bernoulli (1667-1748) propuso en la revista Acta Eruditorum a los matemáticos como desafío el problema de la braquistócrona con estas palabras:
«determinar la curva, entre las infinitas posibles, por la que un cuerpo desciende en el menor tiempo posible entre dos puntos que no estén ni en posición vertical ni horizontal, movido únicamente por efecto de la gravedad«.
Leibniz le sugirió a Bernoulli que invitara a Newton al desafío y el 29 de enero de 1697, E. Halley (1646-1742) le entregó la carta de Bernoulli con el problema a resolver. Newton lo resolvió esa noche y publicó la solución al reto de Bernoulli de manera anónima en la revista Philosophical Transactions de la Royal Society. En la que realizó una brillante y corta demostración, precursora del Cálculo de Variaciones, en la que probaba que la curva braquistócrona era la cicloide.
Cuando Bernoulli vio la solución del problema de la braquistócrona (y de otro más que formaba parte del desafío lanzado) y observó la elegancia y la belleza de la demostración exclamó: es Newton. Y cuando le preguntaron el porqué de su afirmación exclamó: Tanquam ex ungue leonem (“Como se reconoce al león por sus garras”).
Otra propiedad física importante de la cicloide es que satisface la propiedad isócrona o (o tautócrona). Esto significa que cualquier partícula situada sobre una cicloide en puntos diferentes A, B, C, D… y sometida únicamente a la acción de la gravedad invierte el mismo tiempo en llegar al punto más bajo, O, de la cicloide. Es decir, el tiempo de descenso libre de la partícula hasta el punto O, es independiente de su posición inicial.
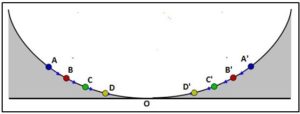
Por lo tanto la partícula, aunque parta de puntos diferentes A, B, C, D, alcanzará los puntos A’, B’, C’, D’ respectivamente en el mismo tiempo. Esta propiedad pendular del movimiento oscilatorio de una partícula sobre la cicloide, por la que el periodo de la oscilación era independiente de la amplitud de la misma fue estudiada por Ch. Huygens (1629-1695), que la aplicó para estudiar el periodo de un péndulo forzado a seguir una trayectoria cicloidal en su obra “Horologium oscillatorium sive de motu pendulorum ad horologia aptato demostrationes geometricae (1673) donde dio una demostración geométrica de este hecho físico.