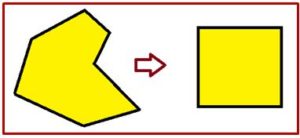
En Geometría, cuando se habla de cuadrar una superficie se entiende que se trata de calcular su área. El término cuadratura procede de la Geometría Griega en la que las áreas de las diferentes figuras se referían al cuadrado, que era el cuadrilátero más sencillo. Y cuadrar una figura era determinar un cuadrado que tuviera la misma área que él. Por esta razón, en los siglos XVII y XVIII se le llamó al Cálculo Integral, con el que se calculaban las áreas de las figuras planas, Método de las Cuadraturas, Un método utilizado por la Geometría Griega para cuadrar un polígono cualquiera se basaba en los procedimientos siguientes:
Procedimiento primero: Cuadrar el rectángulo. Es decir, dado un rectángulo dibujar un cuadrado con la misma área que él.
Cuadrar un rectángulo de base a y altura b se reduce a calcular la media proporcional de los segmentos a y b, es decir, a hallar un segmento x tal que a·b = x2.
Para ello tomamos sobre una semirrecta de extremo A el segmento AB = a y, a continuación, el segmento BC = b. Tomando AC como diámetro dibujamos una semicircunferencia.
En el punto B levantamos una perpendicular que cortará a la semicircunferencia en el punto D y el segmento BD = x es el lado del cuadrado que tiene la misma área que el rectángulo.
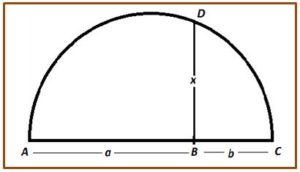
El resultado se basa en el teorema de la altura para el triángulo rectángulo ADC (que es rectángulo en D por abarcar el ángulo inscrito en la circunferencia de 180º), que afirma que la altura relativa a la hipotenusa (BD = x) es media proporcional entre los segmentos en que la divide (a y b), esto es:
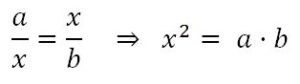
Procedimiento segundo: Hallar un rectángulo que tenga la misma área que un triángulo de base a y altura b.
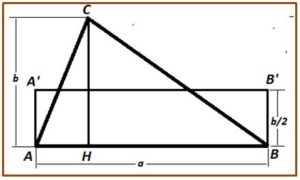
Dado un triángulo ABC de base AB = a y altura BH = b, basta con construir un rectángulo que tenga la misma base AB = a y de altura b/2, tal y como se observa en la figura.
Con estos dos procedimientos podemos abordar el problema básico de realizar la cuadratura de un triángulo de base a y altura b, que consistirá en construir un cuadrado con la misma área que un triángulo dado y se procederá según se observa en la figura siguiente:
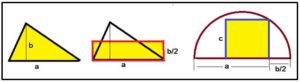
El triángulo de base a y altura b es equivalente a un triángulo de base a y altura b/2, y el lado del cuadrado c es media proporcional entre a y b/2
Procedimiento tercero: Transformar un cuadrilátero cualquiera en un triángulo de la misma área:
Dado un cuadrilátero ABCD, en primer lugar trazamos la diagonal AC y por el vértice D intermedio una paralela a AC, que cortará a la prolongación del lado BC e el punto D’. Tal y como se observa en la figura siguiente:
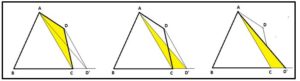
Observemos que los triángulos ADC y AD’C tienen la misma área, ya que tienen la misma base, AC, y también la misma altura, puesto que los vértices opuestos a la base, se encuentran en una recta paralela a la misma. Por lo tanto, si al cuadrilátero ABCD se le quita el triángulo ADC y se le añade el triángulo ACD’ resulta el triángulo ABD’ que tiene la misma área que el cuadrilátero de partida ABCD.
Con este procedimiento se puede cuadrar cualquier cuadrilátero y los anteriores se puede cuadrar cualquier cuadrilátero (cuadrilátero → triángulo → rectángulo → cuadrado)
Procedimiento cuarto: Consiste en aplicar el procedimiento tercero para reducir sucesivamente el número de lados de un polígono hasta llegar al triángulo (Por ejemplo, hexágono → pentágono → cuadrilátero → triángulo) y finalmente cuadrar el triángulo.
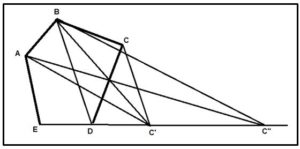
Partiremos del pentágono ABCDE. Trazando la diagonal BD y la paralela a esta diagonal por el vértice C que corta a la prolongación del lado ED en el punto C’ obtenemos el cuadrilátero ABC’E, que tiene la misma área que el pentágono dado. Partiendo ahora del cuadrilátero ABC’E, trazaremos la diagonal AC’ y por el vértice B una paralela a AC’ que corta que corta a la prolongación del lado EC’ en el punto C’’ y el triángulo AC’’E tiene la misma área que el cuadrilátero ABC’E y, por tanto, que el pentágono ABCDE.
Una vez conseguido el triángulo se puede aplicar el proceso anterior. El método general sería como el que se muestra en la figura siguiente, donde todas las figuras destacadas en verde tienen la misma superficie.
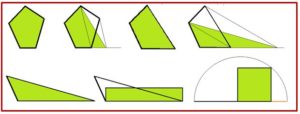
Un método alternativo, y no menos laboriosos, para cuadrar un polígono cualquiera se utilizó en la Edad Media y consistía en dividir al polígono de n lados en n-2 triángulos trazando las diagonales desde uno de sus vértices, para después cuadrar cada uno de los n-2 triángulos por el procedimiento indicado anteriormente y sumar las áreas de los cuadrados obtenidos aplicando el Teorema de Pitágoras.




