
La clasificación de los números según que sus unidades se puedan disponer en triángulos, pentágonos, hexágonos, etc. procede de la Escuela Pitagórica y se mantuvo, a través de las aritméticas medievales escritas por autores latinos, como Boecio (480-524). Estos autores tomaron como modelo la aritmética de Nicómaco de Gerasa (60-120). Los traductores de la Casa de la Sabiduría de Bagdad, escribieron versiones árabes de las obras de matemáticos griegos e indios y enriquecieron la aritmética con el sistema de numeración posicional con las cifras indo-arábigas.
Definición Un número triangular es un número que se obtiene al sumar n números naturales consecutivos y sus unidades se puede disponer formando un triángulo equilátero. Estos números son:
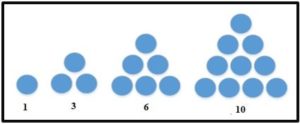
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …, Tn, …
donde Tn es el enésimo número triangular y es la suma de los n primeros números naturales:
Tn = 1 + 2 + 3 + 4 + ··· + n = n(n+1)/2
Propiedad 1.- La suma de dos números triangulares consecutivos es un cuadrado, ya que:
Tn + Tn+1 = n(n+1)/2 + (n+1)(n+2)/2 = 2n2+ 4n+2)/2 = n2+ 2n+ 1 = (n+1)2
Con la representación geométrica de los números se pretendía representar captar la naturaleza de los números, pero no servía para clasificar todos los números en como sucede cuando decimos: números pares e impares, ya que cualquier número o es par o es impar, puesto que, por ejemplo, había números, como el 36, que era triangular y cuadrado.
Propiedad 2.- Los números triangulares están relacionados con los números combinatorios, en realidad el enésimo número combinatorio es igual al conjunto de parejas que se pueden formar con n elementos
![]()
SUMA DE LOS NÚMEROS TRIANGULARES:
Con la suma de los números triangulares {Tn} : 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66,78, …. Se forman los números tetraédricos {TTn} : 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286,…
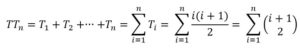
Buscaremos una fórmula para el enésimo número tetraédrico TTn, que supondremos de la forma:
TTn = an3 + bn2 + cn + d
y plantearemos un sistema con T T1 = 1, T T2 = 4, T T3 = 10, T T4 = 20
a + b + c + d = 1 8 a + 4b + 2c + d = 4 7 a+3b +c = 3 27 a + 9b + 3c + d = 10 19 a +5b+c = 6 12 a + 2b = 3 64 a + 16b + 4c + d = 20 37 a +7b +c =10 18 a + 2b =4 6a =1
Y obtenemos:
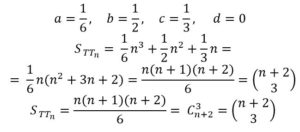
Probaremos por el método de inducción la fórmula combinatoria:

Demostración:
Para n = 1
![]()
Supongamos que se cumple (1) y probemos que se cumple para n+1, esto es:
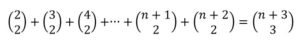
o lo que es igual:
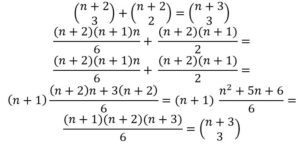
Que es lo que queríamos probar.
Víctor Arenzana Hernández


