
En lenguaje habitual cuando se dice esto es matemático o que algo se cumple matemáticamente significa que algo que es cierto y que está libre de toda duda. Pero, ¿de dónde le viene a las matemáticas esa fama, por otra parte bien merecida, que las han llevado a ser llamadas Ciencias Exactas a ellas y a todas las ciencias que se expresan mediante ellas?
La razón fundamental es que todas las afirmaciones matemáticas están demostradas lógicamente. Y sus pruebas proporcionan confianza que aporta el método axiomático deductivo en el cual, a partir de unos axiomas, utilizando las reglas de la lógica y unos principios generales, se obtienen, resultados proposiciones y teoremas que consideramos válidos.
La palabra demostración ha tenido diferentes significados según en el contexto en el que se haya utilizado. En situaciones informales, puede significar mostrar evidencia visual, probar con la acción que algo se cumple o si algo funciona de una forma determinada. En general podemos quedarnos con la idea de que demostrar algo es mostrar un razonamiento, esquema, analogía o mecanismo capaz de convencernos de su verdad o de su validez
En el caso de la ciencia occidental, las demostraciones matemáticas proceden de la filosofía griega y, más concretamente de la lógica aristotélica, es decir, la ciencia ha optado por el razonamiento deductivo, y se ha asumido como principio incuestionable que la lógica griega forma parte de la naturaleza humana.
Tradicionalmente se pensado en una demostración matemática como un razonamiento que consiste en una sucesión de proposiciones (o fórmulas), en la que cada una de ellas o bien es un axioma o es una consecuencia lógica de las proposiciones (o fórmulas) anteriores.
Una demostración matemática no tiene como conclusión un hecho A (p.e lo que en física sería constatar que el agua hierve), sino que su conclusión es una proposición condicional del tipo si B entonces A (p.e, en física será, si la temperatura alcanza 100ºC el agua hierve). En suma, los teoremas matemáticos son afirmaciones condicionales que dependen de los elementos del sistema axiomático que manejemos.
Estos principios fundamentales de la lógica se identificaron, como hemos señalado antes, con las leyes del pensamiento y, por lo tanto, no se cuestionaron. Dicho de otra manera, no se pusieron en duda simplemente porque eran indiscutibles por estar impresas en nuestra naturaleza.
La demostración euclidiana partía de unos axiomas y, utilizando las leyes de la lógica, obtenía proposiciones, que se empleaban a su vez para demostrar nuevas proposiciones. A continuación, se muestra un ejemplo del rigor axiomático con el que se realiza la demostración de una proposición ( La proposición 6 del Libro I de los Elementos de Euclides) en la que, en el curso de la demostración se indican las proposiciones anteriores en las que se basa la prueba de la misma.
Proposición 6. Si en un triángulo, dos ángulos son iguales entre sí, también los lados que subtienden (lados opuestos) los ángulos iguales serán iguales entre sí.
Demostración: Sea ABC el triángulo que tiene los ángulos ABC y ACB son iguales. Demostraremos que el lado AB es igual al lado AC.
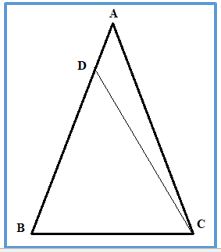
Si AB no fuera igual a AC, uno de ellos será mayor. Sea el mayor AB y, a AB, le quitamos DB igual a AC [Por la Proposición 3 de los Elementos] y se traza DC. (Proposición 3: Dadas dos rectas desiguales, se puede tomar de la mayor una recta igual a la menor)
Como DB es igual a AC y BC es común, los dos DB y CB son respectivamente iguales a los dos AC y CB y el ángulo DBC es igual al ángulo ACB.
Por lo tanto, la base DC es igual a la base AB, y el triángulo DBC será igual al triangulo ACB [Por la Proposición 4 de los Elementos] , es decir, el menor igual al mayor, lo cual es imposible. Luego AB no es desigual a AC. Por tanto, AB y AC son iguales (Proposición 4. Si dos triángulos tienen dos lados del uno iguales a dos lados del otro y tienen iguales los ángulos comprendidos por las rectas iguales, tendrán las bases iguales y un triángulo será igual al otro y, además, los ángulos restantes, a saber, subtendidos por los lados iguales, serán también iguales respectivamente)
No entraremos en este trabajo sobre la evolución de las demostraciones geométricas, ni tampoco en la cuestión de la verdad en matemáticas, temas que surgieron después de la aparición en el siglo XIX de las geometrías no euclidianas, las cuales cuestionaron algunas reglas de la lógica como el principio del tercio excluido. Simplemente haré hincapié en la progresiva complicación de las demostraciones matemáticas. Más allá de la prueba del propio teorema de Pitágoras (proposición 47 del Libro I de los Elementos) que tienía la complicación natural de ser una proposición posterior que se basaba en algunas definiciones, axiomas, y varias nociones comunes (principios lógicos) y utilizaba los resultados de seis proposiciones demostradas anteriormente.
En este artículo atenderemos a la progresiva complicación de las demostraciones deductivas en matemáticas, que, en ocasiones, se requiere la contribución de muchos matemáticos durante mucho tiempo como es el caso del teorema de clasificación de grupos simples, la demostración del teorema de los cuatro colores o la del último teorema de Fermat.
En realidad la demostración completa del teorema de clasificación de grupos finitos simples ocupa alrededor de 15.000 páginas, además, en la prueba realizaron contribuciones más de cien matemáticos. La clasificación y la longitud de la prueba ha hecho que, en determinados momentos, se tuvieran anuncios fallidos de la demostración completa. En 1983 D. Gorenstein (1923-1992) anunció que todos los grupos finitos simples habían sido clasificados, pero esta afirmación resultó prematura, ya que se le había informado mal sobre la prueba de la clasificación del tipo de la clase de grupos quasithin groups (grupos cuasidelgados).

La prueba completa de la clasificación de estos grupos fue realizada en 2004 por M. Aschbacher (1966-) y Smith que publicaron una demostración, de más de mil páginas, en la que clasificaban adecuadamente la clase de quasithin groups.
Con esta demostración la clasificación, se dio por concluida y fue aceptada por la comunidad internacional de matemáticos, hasta el punto que, en 2011, M. Aschbacher fue galardonado con el Premio Rolf Schock de Matemáticas, de la Real Academia Sueca de Ciencias. No obstante, todavía hay matemáticos, como J.P. Serre (1926-), que tienen dudas sobre si la demostración está concluida, porque, dada la extensión y complejidad de la demostración, piensan que podría tener algún vacío más que habría que llenar como ocurrió con los grupos cuasidelgados.
En otras ocasiones ha sido necesario fraccionar el problema en casos distintos y la utilización de una computadora. Como ocurrió con el problema de los cuatro colores planteado en 1852 por F. Guthrie (1831-1899), que se dio cuenta que para colorear un mapa cualquiera de modo que las regiones con una frontera en común tuvieran colores distintos, bastaban cuatro colores ¿serían siempre suficientes cuatro colores para colorear cualquier mapa que imaginemos? .
La prueba de esta conjetura la realizaron en 1976, K. Appel (1932-2013) y W. Haken (1928-) reduciendo el problema a 1482 mapas básicos posibles. Con ayuda de una computadora demostraron que ninguno de ellos necesitaba más de cuatro colores; pero el gran número de operaciones necesarias y la enorme cantidad de tiempo que se emplearon para efectuar los cálculos (1200 horas), unidas a la imposibilidad de que una persona fuera capaz de verificar la prueba de la conjetura manualmente, generó largas discusiones entre los matemáticos sobre si la prueba debía considerarse o no una demostración matemática. No obstante, por ello ganaron el Premio Fulkerson Delbert Ray de la AMS en 1979. Algunos matemáticos llegaron a decir que una demostración matemática era algo así como un poema lógico y que aquella demostración, llena de apartados (al menos 1482) y de largos cálculos, se asemejaba más a una guía telefónica.
Otros problemas cuya demostración es difícil de explicar, no sólo por la dificultad intrínseca de la propia cuestión planteada, sino porque la prueba se realiza en un nivel de abstracción superior y para comprenderla hace falta introducirse en una teoría matemática nueva, diferente de aquella en la que se planteó el problema. Es el caso de la prueba del conocido como último teorema de Fermat (1601-1665), que le surgió cuando estaba estudiando la Aritmética de Diofanto. Fermat, inspirado por las ternas pitagóricas, formuló la siguiente conjetura: es imposible expresar un cubo como suma de dos cubos, una cuarta potencia como suma de dos cuartas potencias o, en general, cualquier potencia de exponente mayor que dos como suma de dos potencias iguales. A lo que añadió un comentario, escrito en el margen de su Aritmética que llevó de cabeza a muchos matemáticos durante más de tres siglos: poseo una prueba, en verdad maravillosa, para esta afirmación a la que este margen es demasiado estrecho.
La lista de matemáticos ilustres que intentaron la demostración es interminable, algunos comprobaron que la conjetura era válida para algunos valores de n, pero ninguno pudo dar con la demostración general hasta que, en 1994, Andrew Wiles (1953-) consiguió demostrar este resultado; aunque no con los métodos que podía conocer Fermat. Wiles echó mano de unas matemáticas del siglo XX para resolver un problema planteado por Fermat en el siglo XVII. Transformó la conjetura de Fermat en un teorema con una demostración de más de cien páginas gracias a teorías matemáticas totalmente nuevas relacionadas con las llamadas curvas elípticas, que están en un nivel de abstracción superior. Para que una persona pueda llegar a comprender la demostración del Ultimo Teorema de Fermat no le bastan los métodos clásicos de la teoría de números, se le debe poner en antecedentes de una nueva teoría, con un elevado grado de abstracción, desde la que se puede abordar la prueba del Teorema.
