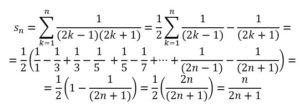El principio de inducción matemática se emplea habitualmente para estudiar la validez de una fórmula que depende de un número natural n. Para reconocer que una fórmula es falsa basta con encontrar un contraejemplo, como ocurre con la fórmula n2 + n + 41, que parece que va a proporcionarnos un número primo para todo valor de n, ya que para los diez primeros naturales obtenemos: 41, 43, 47, 53, 61, 71, 83, 97, 113,131, … , que son todos números primos, pero, sin embargo, no es así, puesto que para n = 40 el resultado es 1681 = 412, que, claramente, no es número primo.
402+40 + 41 = 40 (40+1) + 41= 40·41+ 41 = 41( 40 +1) = 412
Otra suposición curiosa de fórmula válida fue la que se mantuvo durante años con la factorización del binomio xn-1, donde n es un número natural Este binomio fue estudiado por muchos matemáticos, ya que está íntimamente relacionado con el problema geométrico de dividir la circunferencia en n partes iguales (en realidad encierra las raíces de la unidad imaginaria). Los matemáticos estudiaron el problema de descomponer xn -1 en factores irreducibles con coeficientes enteros y observaron que, para muchos valores particulares de n, los coeficientes del desarrollo eran la unidad, en valor absoluto y supusieron que esta propiedad se cumpliría para cualquier n. En efecto, la suposición se verificaba
Para x =1 x – 1 = x + 1,
Para x =1 x2– 1 = (x – 1) (x + 1)
Para x =1 x3 -1 = (x – 1) (x2 + x+1)
Para x =1 x4 -1 = (x-1) (x+1) (x2+1)
Para x =1 x5 -1 = (x-1) (x4 + x3 + x2 + x +1)
·· ··· ···
Se calcularon otras factorizaciones para distintos de valores del exponente n y se observó que los coeficientes de los factores cumplían la propiedad supuesta. Pero la demostración de que esta propiedad era válida en general, es decir, que se cumplía para todo valor de n, no se consiguió fácilmente. El problema fue resuelto por V. Ivanov en 1941, que, sin ordenador ni manipulador algebraico (no existían) encontró un contraejemplo, demostró que la propiedad observada no la cumplían los binomios, de grado es mayor de 105.
Aquí hemos realizado la descomposición en factores con el manipulador simbólico DERIVE y hemos obtenido una factorización en la cual un coeficiente de uno de los factores es -2.
x105 – 1 = (x – 1)·(x2+ x + 1)·(x4 + x3 + x2 + x + 1)·(x6 + x5 + x4 + x3 + x2 + x + 1)·(x8 – x7 + x5 – x4 + x3 – x2 + 1)·(x12 – x11 + x9 – x8 + x6 – x4 + x3 – x + 1)·(x24 – x23 + x19 – x18 + x17 – x16 + x14 – x13 + x12 – x11 + x10 – x8 + x7 – x6 + x5 – x + 1)·(x48 + x47 + x46 – x43 – x42 – 2·x41 – x40 – x39 + x36 + x35 + x34 + x33 + x32 + x31 – x28 – x26 – x24 – x22 – x20 + x 17 + x16 + x15 + x14 + x13 + x12 – x9 – x8 – 2·x7 – x6 – x5 + x2 + x + 1)
Para demostrar que una fórmula es válida podemos usar dos métodos, por ejemplo
Utilizar el método de inducción para hallar una fórmula que proporcione la suma de los n primeros términos de la serie:
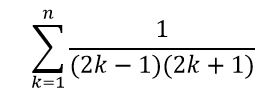
Queremos hallar una fórmula para la suma;
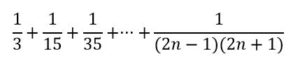
Habra que demostrar la validez general de una fórmula que obtenemos experimentalmente:

Lo que nos sugiere la fórmula
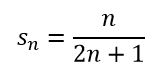
Para demostrar que la fórmula es válida para todo valor de n aplicaremos el método de inducción
- Evidentemente se cumple para n=1

- Supongamos que se cumple para n = k, es decir:
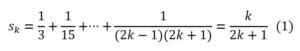
- Demostraremos que, con esta suposición, se cumple para k = k +1, es decir si:
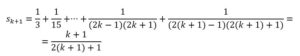
Sustituyendo sk en sk+1, obtenemos:


Que es lo que deseábamos probar.
La fórmula (1) la podríamos haber obtenido por métodos algebraicos utilizando el carácter telescópico de la serie estudiada. Descomponiendo en fracciones simples del siguiente modo: