Un hombre pescaba desde una barca en un río cuya corriente tenía una velocidad de tres kilómetros por hora. El pescador, cansado de dejarse llevar por la corriente y de que los peces no picaran, decidió buscar en el río un sitio mejor para pescar. Puso en marcha el motor de la barca y comenzó remontar la corriente del río. En ese momento el viento le quitó el sombrero, que cayó al agua junto al bote. Pero el pescador no se percató de ello hasta que no estuvo a cinco kilómetros del sombrero. Entonces giró y fue, corriente abajo, hasta llegar a la atura del sombrero que flotaba en el agua. Si cuando no hay corriente, el motor de la barca la impulsa con una velocidad de cinco kilómetros por hora. Si el pescador perdió su sombrero a las dos de la tarde, ¿A qué hora lo recuperó?
Respuesta: La solución de este problema es sencilla, pero resulta interesante acercarse al mismo desde dos puntos de vista:
A) Punto de vista de un observador situado en la ribera del río:
El observador constata que, mientras el sombrero y el pescador se alejan el sombrero desciende a 3km/h y la barca sube contracorriente a 2km/h, es decir, en el momento el pescador se percata de la pérdida del sombrero, que se encuentran a 5 km de distancia y hasta el momento en el que el pescador repara en laa pérdida del sombrro habrán transcurrido un tiempo de t horas , de modo que:
3t + 2t = 5 ⇒ 5t = 5 ⇒ t = 1 hora
Es decir, tarda una hora en darse cuenta.
Igualmente, el observador de la orilla comprueba que cuando el pescador va corriente abajo a buscar su sombrero, momento en que el observado ve que están a 5km de distancia. Desde que el pescador se percata de la pérdida del sombrero hasta lo alcanza, habran transcurrido t’ horas. En ese tiempo el sombrero habrá descendido una distancia 3t’ km y la barca habrá navegado un tiempo 8t’, es decir:
8t’ = 3t’ + 5 ⇒ 5t’ = 5 ⇒ t’ = 1 hora
luego tarda dos horas en recuperar el sombrero
B) Punto de vista de un observador que se mueva con el agua del río y se desplace dejándose llevar por la corriente desde el punto en el que el pescador perdió su sombrero:
El observador constata lo siguiente: que a efectos de cálculo la velocidad del agua no influye en el problema, cuando se aleja el pescador del sombrero lo hace a 5km/h y cuando se acerca también lo hace a la misma velocidad). Por lo tanto observa que:
1.- Cuando pescador se aleja de él (y del sombrero) corriente arriba va a 5km/h y que cuando está a una distancia de 5 km, habrá pasado una hora, es decir, tardará una hora en percatarse de la pérdida del sombrero
2.- Cuando el pescador va corriente abajo a buscar su sombrero recorre otros cinco km respecto al agua en lo que empleará otra hora volver a recogerlo, puesto que la corriente impulsa a los dos.
Por lo tanto, lo mismo en la subida que en la bajada empleó una hora, y+luego si perdió su sombrero a las dos de la tarde, lo recuperará a las cuatro de la tarde.
VIAJE DE IDA Y VUELTA
(Martin Gardner, Matemáticas para divertirse)
El señor Martínez quería viajar de Madrid a Valencia y luego regresar a Madrid. Deseaba hacer el viaje completo a una velocidad media de 120 kilómetros por hora. Al llegar a Valencia descubrió que había realizado el viaje el viaje de ida a una velocidad media de 60 km/h. En primer lugar pensó que haciendo el viaje de vuelta a 180 km/h conseguiría su objetivo, pero luego se convenció de que, cualquiera que fuera la velocidad de vuelta, nunca podría realizar el viaje completo a una velocidad media de 120 km/h ¿Cómo razonó el señor Martínez?
La distancia de Madrid a Valencia es de 360 km. Cuando Martínez llegó a Valencia había recorrido 360 km en seis horas. Como deseaba duplicar su velocidad media de ida y vuelta, lo que necesitaba era recorrer 720 km en seis horas, que ya las había empleado en el viaje de ida a Valencia. Luego debería volver a Madrid en cero segundos y eso es imposible. Por tanto, por mucho que corra el señor Martínez nunca podrá realizar el viaje completo a una velocidad media de 120 km/h.
Si lo hubiéramos planteado matemáticamente para recorrer los 720 km de ida y vuelta emplea 6 horas en la vuelta (360/60) y x horas en la vuelta, lo que da una velocidad de (360/x) km/h. Por lo tanto llevar 120 km/h de velocidad media implica que:
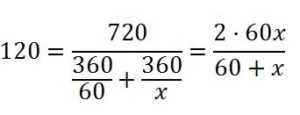Lo que nos lleva al absurdo 120 (60 + x) = 120x ⇒ 60 = 0
Observemos que no es necesario conocer la distancia entre Madrid y Valencia para resolver este problema
