
Aristóteles (384-322 a. de C.) dejó el azar limitado al conjunto de los procesos que carecían de orden, porque carecían de la finalidad que tenían para él los procesos naturales. Aristóteles rechazaba los argumentos de los que mantenían que todo lo que existía se había generado por casualidad y los de aquellos que afirmaban que la suerte, considerada como tal, era una causa, aunque la afirmaba que la suerte tenía algo divino y, tan demoniaco, que la hacía inescrutable al entendimiento humano (Fís.II, 4, 196b).
En la física aristotélica se consideraba que todo lo que sucedía por naturaleza, estaba regido por leyes, era impulsado por las cuatro (material, formal, eficiente y final) y sus efectos se verificaban, tal y como se esperaban, en la mayoría de los casos.
Básicamente, Aristóteles mantuvo que el azar no existía como realidad autónoma porque, incluso en aquellos hechos carentes de finalidad, como era el caso del color de los ojos en la especie humana, no eran fenómenos antinaturales azarosos o sin leyes producidos por el azar, sino que eran realidades no regladas cuyas causas eran indeterminadas o desconocidas, pero que existían.
También aceptaba como forma limitada del azar la casualidad, que se diferenciaba de la suerte, sobre todo, en las cosas generadas por naturaleza; pero cuando resultaba algo contrario a la naturaleza (aparecía algo diferente a lo que naturalmente se podía esperar de ese fenómeno), no decía que se había generado fortuitamente o por suerte, sino por casualidad. En este caso, la causa de un efecto casual era externa, mientras que en la generación contra la naturaleza es interna (Fís.II 6 197b).
Cualquier persona podía observar que en el mundo sucedían hechos azarosos, ya que sucedía, a veces, que algo se había intentado y, sin embargo, no había podido lograrse porque sucedió otra cosa que impidió lograr lo buscado. Otras veces, algo pasaba por casualidad, es decir, cuando sucedía algo que no se esperaba, ni estaba previsto. Frente a esta realidad observable, en el desarrollo de su Física, Aristóteles, optó por considerar el análisis de las cuestiones relativas a los hechos azarosos y casuales concediéndoles un lugar entre los procesos naturales, sin negarlos, pero evitando darles relevancia en el origen del mundo. (Física II, 4, 196a y -196b).

Santo Tomás (1224-1274) incorporó a su filosofía buena parte de la física aristotélica y asumió también la doctrina acerca del azar. Pero, en la cosmovisión cristiana en la que aparece un Dios primer motor, necesario, perfecto, omnipotente, eterno, inmutable y creador y gobernador de mundo parecía imposible encontrarle un lugar al azar en el universo. En un mundo creado por este Dios para el que el pasado y el futuro están presentes, esto es, para el que todo estaba ya previsto y diseñado por él, no había lugar alguno para el fallo ni para la indeterminación características propios del azar.
Llegamos a la Edad Media con un mundo creado por Dios y dotado de unas leyes perfectamente establecidas por el Dios arquitecto; el azar quedaba oculto bajo la alfombra de un pensamiento racional y lógico fuertemente apoyado por la religión, que aportaba la idea de que las leyes de la naturaleza habían sido establecidas por el Dios creador de todo lo que existía y que, por lo tanto, eran leyes inamovible

El azar volvió a resurgir en el siglo XVII al estudiar matemáticamente los juegos de azar. En el estudio se daba por sentado que un mismo experimento podía producir resultados distintos y no se dejaron de estudiar filosóficamente la causa, la suerte y la casualidad, simplemente se analizaron las posibilidades de ganar cada jugador, si un juego era ventajoso, desfavorable o equitativo, en suma, conceptos que podían ser cuantificables. Así comenzaron a estudiar juegos de dados y cartas sin tener en cuenta la causa que podía producir cada resultado y considerando solamente los diferentes resultados que podían aparecer en cada juego.

Leibniz (1746-1716) reconoció el carácter imprevisible de los resultados de los juegos de azar, pero creía en un mundo determinista creado por Dios y cuyo comportamiento estaba regido por unas leyes fijas que se podían expresar en forma de ecuaciones diferenciales. Precisamente en esas ecuaciones acabaría surgiendo el azar, cuando se abordó el estudio del problema de los tres cuerpos; las ecuaciones diferenciales que resumían el estudio determinista de este problema eran sensibles a las condiciones iniciales y sus resultados variaban según la condición de partida.
Pero en los en resultados aleatorios de los juegos de azar también se descubrieron leyes. Esas leyes no eran causales deterministas, en el sentido que no tratan de describir paso a paso el proceso físico, cuando se lanza un dado las leyes del azar no nos dicen el resultado que va salir. Las leyes que tiene el azar se refieren a regularidades que se cumplen en los resultados a largo plazo, Este sentido, al incorporar el tiempo, lo podríamos llamar matemáticas de la historia de la probabilidad de aparición de los diferentes resultados.
La situación en el siglo XVIII estaba en una situación en algunas materias como la astronomía o la mecánica estaban matematizadas y su funcionamiento se podía expresar con fórmulas matemáticas que colmaban el ideal determinista según palabras de Laplace:
“Es nuestro deber considerar el estado actual del universo como un efecto de su anterior estado y como la causa de lo sucederá. Si fuera posible tener por un instante una inteligencia que pudiera abarcar todas las fuerzas que animan a la Naturaleza y la situación respectiva de los objetos que la componen – una inteligencia lo suficientemente grande como para someter al análisis estos datos – comprendería en la misma fórmula el movimiento de los cuerpos más grandes del universo y el del átomo más liviano; para ella nada sería incierto y tanto el futuro, como el pasado, estaría presente ante sus ojos”.
Y, por otra parte, el azar, que no tenía leyes de ese tipo. Sin embargo, hablamos de leyes del azar, aunque estas leyes presentan algunas diferencias con las leyes de mecánica leyes? Pensemos en una diderencia esencial y es que mientras la mecánica clásica
La fotografía y la situación al final de los tiempos Incorpora el tiempo
La ley de los grandes números: Si la probabilidad de éxito en un ensayo de Bernouilli para un suceso A es p la frecuencia relativa de éxitos en un gran número de ensayos será p. Este teorema y sus generalizaciones constituyen algunos de los resultados más importantes de la teoría de probabilidades.
La generalización: si las variables aleatorias x1, x2, x3, … , xn son independientes y todas tienen la misma media, m, y la misma desviación típica, siempre que n sea suficientemente grande existe un probabilidad tan próxima a la unidad como deseemos para que la variable
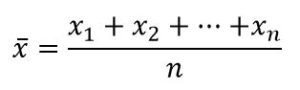
difiera tan poco de m como se quiera, esto es:
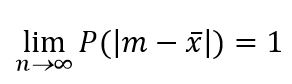
Este resultado justifica la regresión a la media que consiste en que saber que, a largo plazo, a rachas de buena suerte le seguirán periodos de malos resultados, que se pueden traducir en que tras la obtención de un gran número de caras seguidas en el lanzamiento de monedas seguirán etapas de preponderancia de cruces, que a rachas la mano caliente en baloncesto, le seguirán otras de sequía encestadora…
Teorema del límite central es otro principio básico de la estadística, su importancia radica en que es un esquema que se produce en muchos fenómenos del mundo real cuyos resultados dependen del azar. Es una ley que afirma que cuando un fenómeno se encuentra sometido a la influencia de muchas causas (variables aleatorias) independientes dos a dos x1, x2, x3, … , xn, que actúan de forma casual y que, además, cada una de ellas aisladamente ejerce una influencia muy pequeña sobre el fenómeno total entonces, si n es muy grande, la distribución de la suma yn = x1 + x2 + x3 + … + xn, no difiere sensiblemente de una distribución normal.
Precisamente el teorema del límite central es una de las principales causas de la importancia de la distribución normal en estadística.
Por ejemplo, la dispersión del impacto de un cañón respecto al blanco sigue una distribución normal; porque la dispersión depende de muchas variables como irregularidad del proyectil, peso del mismo, cantidad de pólvora, pequeñas variaciones en la velocidad del viento, etc. También aparece el Teorema en la física estadística, en los estudios de mercado o en los procesos de reacciones químicas
La ley de las tres sigmas. Afirma que en una distribución normal de media µ y desviación típica σ el 68% de las observaciones se encuentran dentro de la primera desviación estándar (µ-σ, µ+σ) , el 95% dentro de las dos primeras desviaciones estándar (µ-2σ, µ+2σ) y el 99,7% dentro de las tres primeras desviaciones estándar (µ-3σ, µ+3σ). Esta ley se utiliza como una forma aproximada de probar la normalidad de una distribución. Si demasiados datos caen fuera de los tres límites de desviación estándar, esto implica que la distribución no es normal
Víctor Arenzana Hernández




