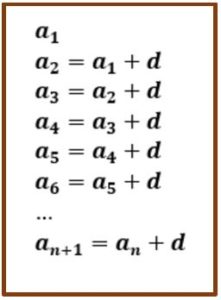
PRIMERO: Determinar si en la progresión aritmética {5n-3}n=1… hay algún término que sea un cuadrado perfecto.
Respuesta: a) En efecto {5n-3}n=1… es una progresión aritmética, ya que la diferencia entre dos términos consecutivos cualesquiera es constante:
an+1– an = 5(n + 1) – 3 – (5n -3) = 5 = d
b) Veamos si existe an = 5n – 3 = a2 : Por ser cuadrado perfecto, a2 puede acabar en {1, 4, 9, 6, 5, 6, 9, 4, 1}, es decir, en las cifras: {1, 4, 5, 6, 9}, y a2 + 3 puede acabar en {4, 7, 8, 9, 2}, pero, esto, entra en contradicción con que el hecho de que:
a2 + 3 = 5n,
ya que a2 + 3 debería ser múltiplo de 5, por lo tanto, tendría que acabar en 0 o en 5 y sólo puede acabar en {4, 7, 8, 9, 2}. Por lo tanto, esa progresión aritmética no tiene cuadrados perfectos.
SEGUNDO.- Determinar si en la progresión aritmética {4n-3}n=1… hay algún término sea un cuadrado perfecto. ¿hay infinitos?
Respuesta: a) En efecto es progresión aritmética, ya que la diferencia entre dos términos consecutivos cualquiera es constante:
an+1– an = 4(n+1) -3 – (4n-3) = 4 = d
b) Veamos si existe an = 4n – 3 = a2 : Los cuadrados acaban en {1, 4, 5, 6, 9}, a2 + 3 puede acabar en {4, 7, 8, 9, 2}, por lo tanto a2 + 3 = 4n debe ser múltiplo de 4 ⇒ n = (a2+3)/4 puede ser entero.
Para n =1 ⇒ an = 1, para n =3 ⇒ a3 = 9, para n = 7 ⇒ a7 = 25, para n = 13 ⇒ a13 = 49, …., que son cuadrados.
La progresión será: 1,5,9,13,17,21,25,29,33,37,41,45,49,53,57,61,65,69,73,77,81,85, …
Para demostrar que tiene infinitos cuadrados perfectos en la progresión aritmética veamos el siguiente ejercicio:
TERCERO.- Demostrar que si entre los infinitos términos de una Progresión Aritmética de números enteros positivos hay un cuadrado perfecto, entonces la Progresión tiene infinitos términos que son cuadrados perfectos.
Respuesta
Sea la sucesión progresión aritmética a1, a2, a3, . . ., an, …, cuya diferencia es d, y supongamos que an es cuadrado perfecto, es decir que an = c2 siendo c entero positivo. Veremos que a partir de ese cuadrado podemos determinar otro cuadrado perteneciente a la misma progresión entre los números siguientes
c2, c2 + d, c2+ 2d, . . , c2 + md …..
Observemos que el número
(c + d)2 = c2 + 2cd + d2 = c2 + (2c + d)d = an + (2c + d)d
Es un cuadrado y que, además, pertenece a la progresión y está situado 2c + d posiciones por delante de an = c2.
Tomando m = 2c + d obtenemos que término de la progresión m posiciones más adelante, que es cuadrado. Este razonamiento se puede repetir indefinidamente con este nuevo cuadrado, con el siguiente… Por lo tanto, existirán infinitos cuadrados perfectos en la progresión aritmética.
Este resultado se puede generalizar a cualquier potencia, por ejemplo:
CUARTO.- Demostrar que si entre los infinitos términos de una Progresión Aritmética de números enteros positivos hay un cubo perfecto, entonces la progresión tiene infinitos términos que son cubos perfectos.
Respuesta:
Sea la sucesión a1, a2, a3, . . ., an, … y supongamos que an es cubo perfecto, es decir que an = c3 y c entero positivo, Veremos que a partir de ese cuadrado podemos determinar otro cuadrado perteneciente a la sucesión entre los números siguientes a
c3, c3 + d, c3+ 2d, . . , c3 + md …..
Observemos que el número
(c + d)3 = c3 + 3c2d +3cd2 +d3 = c2 + (3c2 +3cd+d2)d = an+(3c2 +3cd+d2)d
es un cubo y que, además, pertenece a la progresión y está situado 3c2 +3cd+d2 posiciones por delante de an = c3
Tomando m = 3c2 +3cd + d2 obtenemos que término de la progresión m posiciones más adelante, que es cubo. Este razonamiento se puede repetir indefinidamente con este nuevo cubo, con el siguiente… Por lo tanto, existirán infinitos cubos perfectos en la progresión aritmética.