El problema del caracol en el pozo es un conocido acertijo matemático que apareció en la India y que ha sido propuesto en numerosas aritméticas con datos diferentes en lo que se refiere a la profundidad del pozo y los desplazamientos del caracol. El enunciado es el siguiente:
Un caracol se encuentra en el fondo de un pozo de ocho metros de profundidad. Comienza a subir. Durante el día asciende cuatro metros, pero cuando descansa por la noche se desliza tres metros hacia abajo y todos los días se repite la misma historia ¿En cuántos días podrá salir del pozo?
El razonamiento es sencillo: El caracol saldrá del pozo cuando haya escalado una altura de 8m. A primera vista podemos pensar que, como durante el día sube 4m y por la noche desciende 3m, cada día sube un metro, por lo que tardará ocho días en alcanzar la boca del pozo. Pero no es así, porque al comenzar el quinto día habrá escalado cuatro metros, por lo que le faltan otros cuatro para salir del pozo que los subirá ese día y ya no descenderá más, como se ve, a modo de resumen de la tabla siguiente:

Un problema un poco más complicado aparece en algunas aritméticas y consiste en suponer que el caracol cada día está más fatigado y su ascensión disminuye cada día en un porcentaje fijo determinado, en la forma siguiente:
Un caracol se encontraba en el fondo de un pozo de nueve metros de profundidad. Durante el día asciende cuatro metros, pero cuando descansa por la noche se desliza dos metros hacia abajo. La tenacidad del caracol lo llevó a repetir lo mismo cada día. Sin embargo, empezó a cansarse y cada jornada, después de la primera, subía un 10% menos que la anterior ¿Logrará el caracol salir del pozo?
Teniendo en cuenta que cada día asciende un 10% menos, el primer día ascenderá 4m, el segundo día un 10% menos, es decir, 4·0,9 = 3,6m, el tercero un 10% menos, es decir, 4·0,9·0,9 = 4· 0,92 = 3,24 m y así sucesivamente. Y, cada día, después de cada ascenso, se desliza hacia abajo 2m. Llamando h(n) a la altura que alcanza al final del día n podemos expresar:
Al final del primer día alcanza la altura: h(1) = 4 – 2 m
Al final del segundo día alcanza la altura:
h(2) = 4 + 4·0,9 – 2·2 m
Al final del tercer día alcanza la altura:
h(3) = 4 + 4·0,9 + 4·0,92 – 3·2 = 10,84 – 6 = 4,84 m
Al final del cuarto día alcanza la altura:
h(4) = 4 + 4·0,9 + 4·0,92 + 4·0,93 – 4·2 = 13,76 – 8 = 5,76
Al final del quinto día alcanza la altura:
h(5) = 4 + 4·0,9 + 4·0,92 + 4·0,93 + 4·0,94 – 5·2 =16,38 = 6,38
Al final del sexto día alcanza un la altura:
h(6) = 4 + 4·0,9 + 4·0,92 + 4·0,93 + 4·0,94+ 4·0,95m – 6·2 = 18,74 – 12 = 6,74.
Al final del séptimo día se queda la altura:
h(7) = 4 + 4·0,9 + 4·0,92 + 4·0,93 + 4·0,94+ 4·0,95+ 4·0,96m – 7·2 = 20, 86 -14 = 6,86 m
Al final del octavo día se queda la altura:
h(8) = 4 + 4·0,9 + 4·0,92 + 4·0,93 + 4·0,94+ 4·0,95+ 4·0,96+ 4·0,97 – 8·2 = 22,78 -18 = 6,78
Puede observarse que el séptimo día acaba una de altura 6,86 y el octavo a una altura inferior de 6,78 m. luego, a partir del séptimo día, es menos lo que asciende durante el día que lo que desciende al descansar durante la noche. Por consiguiente, la máxima altura la alcanzará el séptimo día (antes de descansar durante la noche) y será de 8,86m. Por lo tanto, como el pozo es de 9m, el caracol no podrá salir de él.
El problema se puede abordar de una forma más directa realizando la suma de todas sus ascensiones en n días que será: h(n) = 4 + 4·0,9 + 4·0,92 + 4·0,93 + ··· + 4·0,9n-1 y quitarle la suma de sus descensos nocturnos, que será 2·n. Expresado de forma compacta se puede expresar así:
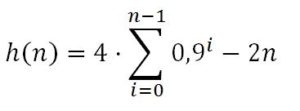
El caracol podrá seguir ganando altura diariamente mientras la altura que asciende durante el día n que sea mayor que la que desciende en la noche de ese día, es decir, si:
4·0,9n-1 > 2 ⇒ (n-1)·log 0,9 > log (1/2)

n < 7,5788, lo que implica que después del séptimo día no gana altura. Al final del séptimo día
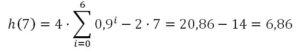
Pero habrá alcanzado dos metros más, es decir, 8,86m