El pentágono regular tiene unas propiedades interesantes algunas de las cuales mostramos continuación:
Propiedad 1.- El ángulo central es de 72º
Indicación: Basta que el pentágono es inscriptible en la circunferencia y mide 360/ 5
Propiedad 2.- El ángulo interior es de 108º.
Demostración: Basta considerar que los lados del ángulo interior del pentágono abarcan las 3/5 partes de su circunferencia circunscrita es decir 216º. Luego el ángulo, que está inscrito en ella medirá la mitad, esto es, 108º
Propiedad 3. Las diagonales que parten de un vértice trisecan el ángulo interior.
Demostración: El triángulo ABC verifica que el Angulo ABC = 108º y, como es isósceles: Angulo BAC = Angulo BCA = 36º, por lo tanto: Angulo ABE = Angulo EBD = Angulo DBC = 36, por lo tanto, las diagonales trisecan el ángulo interior
Propiedad 4.- Los triángulos que determinan en un pentágono regular los lados con sus diagonales son todos isósceles
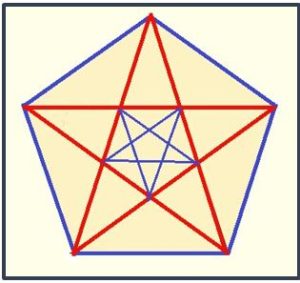
PENTÁGONO REGULAR CON SUS DIAGONALES:

¿Cuántos triángulos se determinan los lados de un pentágono regular y sus diagonales?
Claramente, las diagonales del pentágono regular ABCDE forman al cortarse un pentágono regular invertido 12345. El criterio que seguiremos, para contar todos los triángulos, es identificarlos por el lado desigual, que habitualmente llamamos base del triángulo isósceles.
Primero: Triángulos con base un lado del pentágono ABCDE y el vértice opuesto a la base en el pentágono pequeño 12345: Hay tres triángulos por lado, por ejemplo, para el lado AB, los triángulos AB5, AB1 y AB2, por lo tanto, de este tipo de triángulos, hay: 3·5 = 15 triángulos.
Segundo: Triángulos con base un lado del pentágono ABCDE y el vértice opuesto a ese lado en el mismo pentágono. Hay uno por cada lado, por ejemplo, para el lado AB, el triángulo ABD, por lo tanto, de este tipo de triángulos, hay: 1·5 = 5 triángulos
Tercero: Triángulos que tienen dos lados (necesariamente consecutivos) del pentágono ABCDE.: (Tienen por base sus respectivas diagonales). De estos hay 5 triángulos. Cuarto: Triángulos isósceles que tienen por base una diagonal el vértice opuesto es un vértice del triángulo 12345, por ejemplo, para la diagonal AC el triángulo AC4) lados del polígono… Hay 5. (Los triángulos de lados dos diagonales están contados en segundo apartado).
Quinto: Por último, cinco triángulos que tienen por base un lado del triángulo 12345 y el vértice opuesto es un vértice del pentágono ABCDE, por ejemplo, 12B, de estos hay 5 triángulos.
Luego, en total, el pentágono con sus diagonales tiene 15 + 5 + 5 + 5 + 5 = 35 triángulos.
PENTÁGONO DOBLEMENTE ESTRELLADO
¿Cuántos triángulos se pueden contar en la figura siguiente?
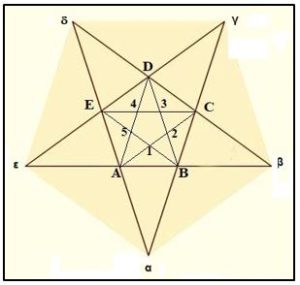
Evidentemente, la figura está formada por el pentágono regular ABCDE y sus diagonales. Acabamos de ver que en esa figura se forman 35 triángulos, ahora tenemos que contar cuantos triángulos nuevos nos aportan en era figura las letras αβγdε.
Se forman triángulos con dos letras griegas (en la misma recta) y una latina, por ejemplo, con dβ y el vértice A, se forma el triángulo dβA. Luego habrá 5 triángulos
Cuatro por cada letra griega y dos latinas, se forman cuatro triángulos: dED, dEC, dAC dDA en total habrá 4·5 = 20 triángulos.
Luego hay 25 nuevos triángulos y en total: 35 + 25 = 60 triángulos
Víctor Arenzana Hernández