La raíz cuadrada de un número natural que no sea cuadrado o la raíz cúbica de un número natural que no sea cubo será un número real irracional y su expresión numérica tiene una expresión decimal no periódica de infinitas cifras. Cuando nos encontramos con expresiones radicales algo complicadas, como las que se utilizan, por ejemplo, en la fórmula de resolución de la ecuación cúbica obtenida por G. Cardano (1501-1576). Los algebristas italianos observaron con sorpresa que algunas ecuaciones cúbicas tenían la particularidad de que, aun teniendo los coeficientes enteros y una solución entera y positiva, la expresión de sus soluciones obtenida con las fórmulas de Cardano tenía una expresión radical tan complicada que era difícil sospechar que en ella se encerrara un número entero, y la sorpresa aun fue mayor cuando la ecuación tenía una solución entera y en la fórmula aparecían raíces cuadradas de números negativos.
A continuación, ponemos dos ejemplos delos problemas de cálculo con los que se encontraron los algebristas del siglo XVI, del tipo de los que los llevaron a extender las operaciones algebraicas a conjuntos numéricos más amplios y a descubrir los números complejos:
Ejemplo l.
La ecuación x3 + 6x = 20, trivialmente, admite la solución x = 2, ya que sustituyendo el valor en la ecuación se puede comprobar que: 23 + 6·2 = 20. Sin embargo, aplicando la fórmula de Cardano para resolver las ecuaciones cúbicas del tipo x3 + px = q, que es:

Obtenemos el siguiente valor de x:
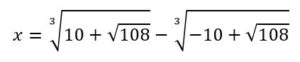
Haciendo el cálculo con calculadora se obtiene:
![]()
≈ 2,7320 – 0,7320 ≈ 2
Aunque, sin demasiados remilgos, se puede admitir que x = 2, demostrar con cálculos algebraicos que esa expresión es exactamente dos permitió avanzar en los cálculos aritméticos y extender las reglas de ls operaciones aritméticas al cálculo literal. Puede demostrarse algebraicamente que es exactamente 2 con los siguientes cálculos:
Recordando que: (a – b)3 = a3 – b3 – 3a2·b + 3 a·b2 calculemos x3 hasta que encontremos x en el desarrollo:
![]()
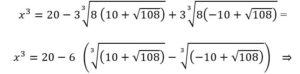
Expresión en la que ha aparecido x ( la diferencia de raíces cúbicas) y obtenemos la ecuación:
Esta ecuación tiene solamente una raíz real, que es x = 2 ya que:
x3 + 6x – 20 = 0 ⇒ (x – 2) (x2 + 2x + 10) = 0
y tiene la solución real x = 2 y las soluciones x = 1 ∓ 3i, de dónde
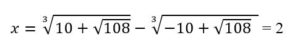
Ejemplo 2: x3 − 15x= 4
Cardano observó, a simple vista, que la ecuación x3 = 15 x + 4 tenía la solución x = 4, con lo que pudo factorizar el trinomio x3 – 15 x – 4 = 0 y obtener que:
x3 – 15 x – 4 = (x-4)( x2+4x+1) = 0
luego resolvió la ecuación de segundo grado x2+4x+1 = 0 y obtuvo otras dos soluciones, que también eran re reales:
x= -2+√3 y x= -2-√3
G. Cardano, en su Ars Magna (1545), también encontró la solución de la ecuación cúbica del tipo: x3 = px + q que se resolvió con la regla:
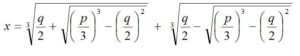
Al aplicársela a la ecuación x3 = 15x + 4 obtuvo la sigunete expresión en la que aparecían raíces cuadradas de números negativos:
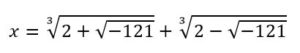
Cardano sabía que esta ecuación tenía las raíces, ya que x = 4 verificaba la ecuación y que no existían las raíces cuadradas de números negativos , pero aparcó el problema.
Esta misma ecuación la tomó R. Bombelli (1526-1572) e intentó dar a la expresión de la solución de la misma, una forma en la que no tuviera influencia el resultado en el que intervenía la raíz de un número negativo en la forma siguiente:
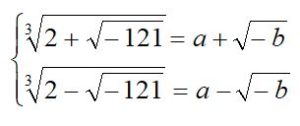
Evidentemente, al sumar las igualdades, miembro a miembro, desaparecería √-b y quedaría que:
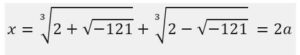
Elevando al cubo:
2 + √(-121) = [a+√(-b)]3 = a3 + 3a2√(-b) + 3a√(-b)2 + b√(-b)
2 – √(-121) = [a-√(-b)]3 = a3 – 3a2√(-b) + 3a√(-b)2 – b√(-b)
Sumando miembro a miembro obtenemos:
4 = 2a3 – 6ab ⇒ 2 = a3 – 3ab ⇒ 2 = a (a2 – 3b)
Calculando, Bombelli obtuvo: que a = 2 y b = 1, con lo que obtenía que la solución era:
x = 2a = 4.
Lo que mostraba una relación entre los números reales y los complejos. Y concluyó que con los números complejos funcionaban las mismas reglas de cálculo que los números reales:
![]()
Bombelli demostró que: si llamamos i = √(-1), entonces √(-121) = 11i y, por tanto:
(2 + i)3 = 8 + 12i – 6 – i = 2 + 11i
(2 – i)3 = 8 – 12i – 6 + i = 2 – 11i
o que 2 + √-121 = (2+√-1)3 y 2 – √-121 = (2-√-1)3.
Bombelli, aplicando las reglas adecuadas de suma y multiplicación, encontró soluciones que hasta entonces no se entendían. Así lo recoge A. Girard (1595-1632) en su libro L’invention Nouvelle en L’algèbre (1629) en el que denominó la extensión de las propiedades de las operaciones de los números reales a los números complejos como principio de permanencia, según el cual todas las identidades algebraicas empleadas en el cálculo con números reales podían emplearse en el cálculo con números complejos. El Álgebra daba más de lo que se le pedía y fue aceptado por muchos matemáticos como una muestra de la generosa generalidad del Álgebra.