¿Cómo podemos saber que una fórmula aritmética es siempre cierta? Podríamos hacer una demostración lógica, entendiendo con ello que estamos dentro de un sistema axiomático y obtenemos la fórmula a partir de los postulados del sistema y siguiendo las reglas deductivas.
Si la fórmula depende de n∈N podemos comprobar si la fórmula es válida, pero es imposible comprobarla para cada n particular, es decir, si se cumple para todos los números naturales o sólo para algunos como exige una demostración matemática porque N es infinito. La inducción es un tipo de razonamiento lógico que permite hacer demostraciones para cualquier valor de n un tiempo finito.
Una demostración por inducción tiene dos pasos:
- (La base de la inducción) Comprobar que la afirmación es cierta en el primer caso.
- (El paso de inducción) Suponer que la afirmación es cierta en un caso cualquiera, k, y, con esa suposición, demostrar que debe ser cierta en el siguiente caso, k+1.
El esquema lógico es el siguiente: si podemos demostrar que una fórmula es cierta para un primer caso, n = 1 y, si, además, podemos demostrar que siempre que la fórmula se verifica para un caso también se verifica en el caso siguiente, entonces por cumplirse para n = 1, se cumple para n = 2, por cumplirse para n = 2, se cumple para n = 3 y así sucesivamente, por lo tanto, la fórmula se cumple para todo n.
EJEMPLO PRIMERO.- Probar que la suma de los cubos de tres números naturales consecutivos cualesquiera es múltiplo de 9.
Solucion : Sea f(n) = n3 + (n+1)3 + (n+2)3 y veamos que f(n) es un múltiplo de nueve para todo n
Paso 1.- Se cumple para n= 1: f (1) = 13 + 23 + 33 = 36, que es múltiplo de 9
Paso 2.- Suponemos f(k) = k3 + (k+1)3 + (k+2)3 es múltiplo de 9 y (cn esta suposición) demostraremos que f(k +1) = (k+1)3 + (k+2)3 + (k+3)3 es múltiplo de 9.
Para eso basta ver que la diferencia f(k +1) – f(k) es múltiplo de 9. Que lo es en efecto:
f(k +1) – f(k) = (k+3)3 – k3 = 3 k2·3 + 3·k·9 +27 = 9(k2 + 3·k +3)
que es múltiplo de 9. Porlo tanto la suma de los cubos de tres números naturales consecutivos cualesquiera es múltiplo de 9.
EJEMPLO SEGUNDO.- Prueba, usando el principio de inducción matemática, que para todo número natural se verifica que n5 – n es divisible por 5.
Solución: Sea la f(n) = n5 – n y demostraremos por inducción que f(n) un múltiplo de cinco
Paso 1.- Sea n = 2, f (2) = 25 – 2 = 30, que es divisible por 5
Paso 2.- Suponemos f(k) = k5 – k divisible por cinco. Con esta suposición demostraremos que
f(k +1) = (k+1)5 – k – 1 es divisible por 5
Para eso basta ver que la diferencia f(k +1) – f(k) es divisible por 5. Desarrollando el binomio y simplificando:
f(k +1) – f(k) = (k5 + 5k4 +10k3 +10 k2+ 5k + 1) – k – 1 – k5 + k =
= 5k4 + 10k3 + 10 k2 + 5k = 5 (k4 + 2k3 + 2 k2 + k)
que es múltiplo de cinco y, por lo tanto, n5 – n es divisible por 5.
EJEMPLO TERCERO.- Un caso que parece sorprender es que f(n) = n2 + n + 41 no genera siempre números primos, aunque los genera para n = 1, 2, …. 39
En efecto son primos f(1) = 41, f(2)= 47, f(3)= 53, f(4)= 71, … f(10) = 151, …., f(39) = 1601
Lo que hace pensar que cumplirá la fórmula dará continiamente números primos, pero no, ya que
f(40) = 402+40+41 = 40·41+41= 41(40+1) = 412, que, evidentemente no es primo.
Se puede demostrar que ninguna expresión polinómica dará números primos para todo valor de n.
en erte caso f(41), f(412), f(413)… son numeros compuestos
EJEMPLO CUARTO.- Prueba, usando el principio de inducción matemática, que para todo número natural n ∈N se verifica la igualdad siguiente.
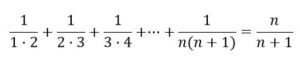Solución: (observemos que n es el número de sumandos)
Si k =1
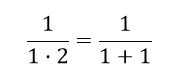Suponemos que la igualdad se cumple se cumple para n = k, es decir:
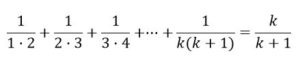
A partir de ella demostraremos que se verifica cuando n = k+1, es decir que:
Luego se cumple.
