https://www.euroresidentes.com/suenos/diccionario_significado_de/a/sonar-con-arana.htm
Todo el mundo conoce que la distancia más corta entre dos puntos de un plano es la línea recta, pero si alguien se viera obligado a caminar sobre una superficie esférica la línea más corta entre dos puntos no podría ser una recta y el camino más corto será el arco de círculo máximo que los une. Se llama geodésica sobre una superficie a la línea más corta trazada sobre la superficie que une dos puntos de la siperficie .
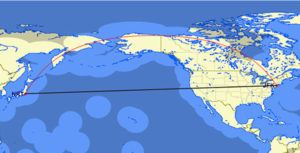
La geodésica para un avión que cubriera el vuelo de Nueva York a Tokyo, ciudades que tienen con una diferencia de longitud geográfica de unos 150º no puede ser una trayectoria recta, la trayectoria no es tan intuitiva y el avión debe ir, si quiere seguir la línea de mínima distancia, un arco de círculo máximo terrestre.
http://jesusgonzalezfonseca.blogspot.com.es/2010/09/cuando-la-linea-recta-no-es-el-camino.html
A continuación proponemos dos sencillas cuestiones que ponen de manifiesto cuál es la línea geodésica entre dos puntos cuando un móvil se mueve sobre una superficie formada por dos planos en ángulo recto.
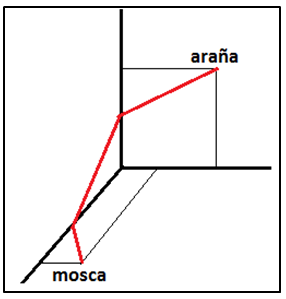
Cuestión 1.- En una pared vertical y a 5 dm del suelo está apostada una araña y en el suelo, pegada a la pared en la que se encuentra la araña y a 5 dm a la izquierda de la vertical de la araña, hay una colilla. Y a 7 dm de la pared y de la colilla se encuentra en el suelo una mosca, tal y como se observa en la figura siguiente:
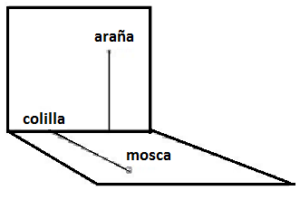
a) ¿Cuál será la trayectoria de la araña y cuál será la mínima distancia que tiene que recorrer para comerse a la mosca? (la araña camina y lo hace sobre los dos planos)
b) ¿A qué punto de la intersección del suelo con la pared se debe dirigir la araña para hacer el recorrido mínimo?
Respuesta: Para determinar la mínima distancia basta con abatir el plano vertical, sobre el que se encuentra la araña, sobre el plano horizontal, mediante un giro de 90º. En esta situación, es evidente que la trayectoria de mínima distancia será el segmento rectilíneo que une el punto A de la figura, en el que se encuentra la araña, con el punto M en el que se halla la mosca.
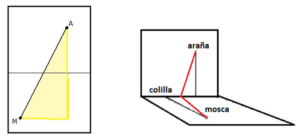
Para que la araña vaya desde el punto A hasta el punto donde se encuentra la mosca M debe recorrer la hipotenusa del triángulo rectángulo sombreado, cuyo cateto vertical mide 12 dm y el horizontal 5 dm, luego debe recorrer una distancia:
Y teniendo en cuenta la semejanza de triángulos,
Luego, por semejanza de triángulos, se obtiene el punto x el suelo al que debe dirigirse la araña :
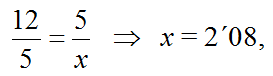La araña debe dirigirse a un punto situado a 2’92 dm de la colilla situada en el suelo.
Cuestión 2.– En una pared vertical y a 5 dm del suelo y a 3 dm de una pared lateral hay una araña. En el suelo, a 7 dm de la pared en la que se encuentra la araña y a 1 dm de la pared lateral se encuentra una mosca
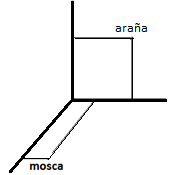
¿Cuál es la mínima distancia que tiene que recorrer la araña para comerse a la mosca?
¿A qué punto de la intersección del suelo con la pared se debe dirigir la araña?
La araña, como no puede volar, tiene, en este caso, la opción de pasar por dos o tres de los planos que forma el rincón donde se encuentra . Para determinar el camino de mínima distancia, esto es, la geodésica entre la araña y la mosca procederemos de forma análoga al caso anterior, pero, así como en ese caso había una sola posibilidad de abatir el plano sobre el plano horizontal ahora cabe tres posibilidades se gú el eje que elijamos como eje de giro del abatimiento
Podemos hacer el desarrollo de las siguientes formas:
a) Cortando el eje OX y abatir sobre el plano YZ como en el caso a) de la figura siguiente.
b) Cortando el eje OY y abatir sobre el plano XZ, como el caso b) de la figura.
c) Cortando el eje OZ y abatir sobre el plano XY, caso c).
Puede comprobarse que se obtienen los siguientes resultados
Puede comprobarse que se obtienen los siguientes resultados
Luego en el caso b), en el cual la araña camina por las tres paredes es el recorrido de menor distancia Aplicando la semejanza de triángulos, se puede calcular fácilmente:
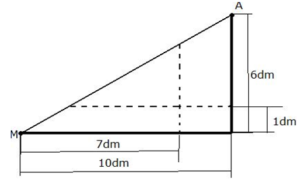
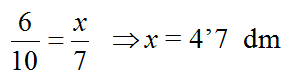
se dirige a un punto de la arista vertical situado a 3´7 dm del suelo.
Fig 6-2. La araña
y luego se dirige a un punto de la arista horizontal a 5’3 dm del rincón. Aproximadamente como se indica en la figura siguiente:
