La estrella de ocho puntas se obtiene por la superposición de dos cuadrados concéntricos cuando uno de ellos ha sido girado 45º respecto al otro. Su origen se remonta los símbolos religiosos de antiguas civilizaciones mediterráneas, como la Tartesia (en Andalucía), también aparece en la Biblia y se la conoce como Estrella de Salomón. Platón la llamó Estrella Gadeira haciendo alusión a su procedencia gaditana. En la Edad Media se la conoció como Estrella de Abderramán I (731-788) , primer califa del Al-Ándalus, el cual la extendió por todos los países costeros del Mediterráneo.
En el Reino de Granada pasó a formar parte de la decoración de las fachadas de edificios, de ilustraciones, de grabados, del diseño joyería, etc. Los mozárabes y mudéjares difundieron la estrella de ocho puntas por buena parte de España y los musulmanes y moriscos la extendieron por el Magreb.
La estrella de ocho puntas se puede construir a partir de la descomposición de una circunferencia en ocho partes iguales o, lo que es igual, a partir del octógono regular. Como a partir de un mismo conjunto de puntos se pueden obtener estrellas diferentes, para denominarlas específicamente se suele utilizar la notación de Schläfli, (n / q) donde n es el número de vértices del polígono regular del que procede y q–1 es el número de vértices que nos saltamos en cada paso para unir dos vértices (o que q es el número de lados del polígono intermedios entre los extremos de la diagonal)
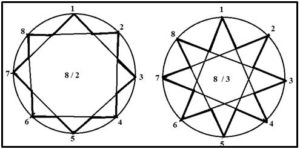
En la figura anterior podemos observar las dos estrellas que es posible formar a partir de los vértices del octógono regular la 8 /2, la de la izquierda, se forma partiendo de un vértice, dejando un vértice entre los extremos de la diagonal del octógono, hasta recorrerlos todos. Se obtienen las dos secuencias cíclicas: 1 ⤍ 3 ⤍ 5 ⤍ 7 ⤍1 y 2 ⤍ 4 ⤍ 6 ⤍ 4 ⤍ 1 y la estrella resulta como intersección de dos cuadrados uno de ellos girado 45º.
La estrella de la derecha, la 8 /3, se forma partiendo de un vértice, dejando dos vértices entre los extremos de la diagonal y se obtiene la secuencia: completa de los ocho vértices: 1 ⤍ 4 ⤍ 7 ⤍ 2 ⤍ 5 ⤍ 8 ⤍3 ⤍ 6 ⤍1.
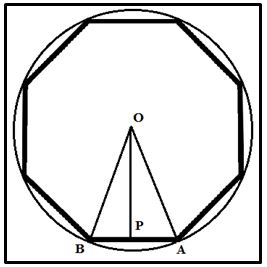
1.- Área del octógono regular. Si el radio del octógono es OA = 1, como el ángulo BOA vale 45º y sen 45º = cos 45º = √2/2 y teniendo en cuenta las fórmulas trigonométricas del ángulo mitad. El lado del octógono, BA, será igual a 2 OA · sen (45º/2):

Y la apotema OP = OA · cos (45º/2)

El área del octógono se calcula por la conocida fórmula: Perímetro · Apotema /2:
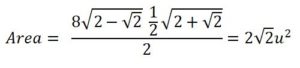
2.- Área de la estrella 8 / 2, formada por dos cuadrados. Será el área de un cuadrado de lado √2 más dos cuadrados de lado x , que cumple:

2x + x√2 = √2 ⇒
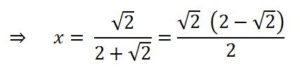
Los dos cuadrados de lado x tienen área igual a
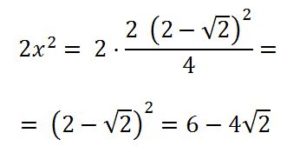
Área de la estrella 8/2 = 2 + 6 – 4√2) = 8 – 4√2 u2
Perímetro de la estrella 8/2 = 16x = 8√2 (2 – √2) = 8 (2√2 – 2) = 16 (√2 – 1)
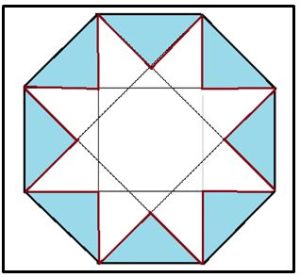
3.- Área y perímetro de la estrella, 8/3. De la figura se deduce que el área encerrada por el contorno de las estrella será igual al área del octógono, 2√2, menos el área de cuatro cuadrados (azules) cuya diagonal es el lado del octógono, o, lo que es igual, menos dos cuadrados de lado el lado del octógono, es decir :
Área de la estrella 8/3 = 2√2 – 2·(2- √2) = 4√2 – 4 u2
Del lado del octógono calculado antes se obtiene trivialmente que el lado de la estrella 8/3 de 16 lados es