Desde el siglo XIX en matemáticas se maneja con total naturalidad la noción de ley de composición (operación binaria) en un sentido más amplio que el que se venía manejando hasta entonces. La suma de números enteros es una ley de composición (interna), porque asocia a cada par de números enteros otro número entero, es decir la suma (S) es una correspondencia que a cada par de enteros a y b le hace corresponder el entero a+b. En forma: esquemática:
S: Z x Z → Z, tal que a cada (a , b) → a+b.
Otros ejemplos son: la suma en los racionales o la suma y el producto de números complejos etc. Podemos pensar, por tanto, que las leyes de composición eran conocidas desde los comienzos de las matemáticas, ya que las operaciones aritméticas lo son, pero, en aritmética eran consideradas como operaciones con números con un significado físico concreto y en Algebra como expresiones literales cuyas variables representaban números (y, más precisamente, números algebraicos).
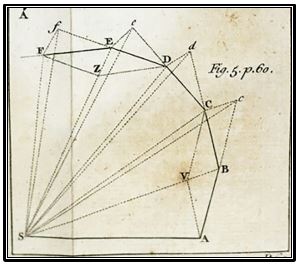
En algunas ocasiones se ha creído encontrar antecedentes anteriores al siglo XIX de la noción ampliada de operación aritmética. Ejemplos como la regla del paralelogramo utilizada por I. Newton (1643-1727) parece indicar que el científico inglés manejó la suma de vectores. Realmente se sirvió de la Regla del Paralelogramo para demostrar que las órbitas de los planetas eran elípticas (El planeta en ausencia de fuerzas seguiría una trayectoria rectilínea (Ley I del Movimiento, Principio de Inercia), pero la fuerza atractiva del Sol (Por la Ley II le hace cambiar de dirección del movimiento según la según la Regla del paralelogramo. También la utilizó para demostrar de forma matemática las Ley de las Areas formulada por Kepler
Las Leyes de Movimiento Newton las formuló así:
Ley I.- Todos los cuerpos perseveran en su estado de reposo o de movimiento uniforme en línea recta, salvo que se vean forzadas a cambiar de su estado por fuerzas impresas.
Ley II.- El cambio de movimiento es proporcional a la fuerza motriz impresa y se hace en la dirección de la línea recta en la que se imprime esa fuerza.
La Regla de Paralelogramo aparece formulada específicamente en los Principia en el Corolario Primero, tras la tercera Ley de Movimiento en la siguiente forma:
Corolario primero: Un cuerpo afectado por dos fuerzas describirá la diagonal del paralelogramo en el mismo tiempo que describiría los dos lados de ser afectado separadamente por ambas fuerzas
Si, en un momento dado, un cuerpo fuese llevado con movimiento uniforme por la fuerza M impresa en el lugar A, desde A hasta B y, en el mismo lugar fuese llevado de A a C, y con ambas fuerzas actuando a la vez completamos el paralelogramo ABCD, y el cuerpo será llevado en el mismo tiempo por la diagonal desde A hasta D.
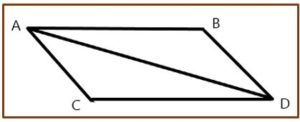
Dado que la fuerza N actúa en la dirección de la línea AC, paralela a BD, esta fuerza, por la Ley II, no alterará para nada la velocidad generada por la otra fuerza M, mediante la cual el cuerpo es llevado hasta la línea BD. En consecuencia, el cuerpo llegará a la línea BD en el mismo tiempo, esté impresa o no la fuerza N y al terminar ese tiempo se encontrará en algún punto de la línea BD. Por el mismo argumento, al final del mismo tiempo, se encontrará en algún punto de la línea CD, en consecuencia, se encontrará en el punto D, donde ambas líneas se cortan, pero se moverá en línea recta por la Ley I.
Indudablemente está utilizando la Ley del Paralelogramo de la suma de vectores, pero no se puede considerar que tal operación concebida por Newton sea una ley de composición en el sentido de ser una extensión de las leyes numéricas, ya que el razonamiento no es matemático sino derivado de unas leyes mecánicas y, además, el conjunto en el que está definido ley del paralelogramo no está definido.
El éxito del Cálculo Infinitesimal y sus aplicaciones a la Mecánica hizo que la mayor parte de los matemáticos se dedicaran a su estudio y desarrollo y que se abandonara el Algebra Pura y que no se profundizara en lo que significaban las sucesivas extensiones numéricas y las extensiones de las operaciones algebraicas a los diferentes tipos de números para poder comprender el significado de Ley de Composición (u operación binaria) como concepto independiente. Sin embargo, a partir de 1800, con la representación geométrica de los números complejos, se empezó a vislumbrar la suma de vectores en el plano y a explorar la posibilidad de extender las operaciones con números complejos a otro tipo de “números” que desempeñaran el mismo papel en el espacio que ellos: los cuaterniones, que abrieron el camino del algebra lineal. Los cuaterniones, definidos por W. R. Hamilton (1805-1865) en 1843, y, del mismo modo que los números complejos eran una extensión de los números reales añadiéndoles una unidad imaginaria que cumplía i 2 = -1, los cuaterniones eran un conjunto: H ={a + bi + cj +dk}, donde eran números reales y las tres unidades imaginarias cumplían i2 = j2 = k2 = ijk = -1.
La resolución de ecuaciones mediante radicales de ecuaciones algebraicas de grado mayor o igual que cinco llevó a investigar la “Teoría de Sustituciones” partiendo de las ideas de J.L. Lagrange (1736-1813), A. Vandermonde (1735-1796) y K.F. Gauss (1777-1855) y culminando con las ideas de N. Abel (1802-1829) y E. Galois (1811-1832) que asociaron la solución por radicales de ecuaciones con el grupo de permutaciones asociado a ellas. Con ellos aparece producto de sustituciones y aunque se conocía la composición de funciones, el aspecto algebraico de esta ley de composición y su relación con el producto de dos permutaciones aparecen por primera vez en los trabajos de Abel y Galois. Y fueron difundidos en las obras de J. A. Serret (1819-1895) Cours d’Algebre superieur (1849) y de C. Jordan (1838-1922) Traité des substitutions et des équations algébriques (1870).
Las sustitucines inicialmente no fueron consideradas como elementos, de haber sido consideradas de este modo la aplicación sicesiva de sustituciones se podía haber considerado como una operación y se habrian descubierto operaciones no commutativas como el producto S3 era no com elemento:
![]()