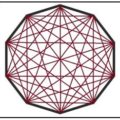
La expresión Pons Asinorum (Puente de los Asnos) era una expresión de la escolástica latina que se aplicaba a determinadas partes de las disciplinas científicas, a ciertos temas de lógica y de la filosofía y a otras cuestiones del aprendizaje, que presentaban para algunos estudiantes una dificultad tan grande que, en ocasiones, les hacían perder el ánimo para seguir cursando esa materia. Así queda reflejado en el grabado que se muestra arriba en el que, a una determinada altura , sobre columnas, están los esquemas de los métodos de la argumentación lógica de Aristóteles, por debajo los que no superaban esos conocimientos que están representados con asnos, mientras que el que los había superado se elevaba a las alturas de la gloria. No obstante, esta expresión (Pons asinorum) se suele utilizar (con matices) para referirse a una prueba o test elemental de conocimientos, o de habilidades en una materia que si no es superada demostraba la falta de capacitación en esa materia, y no se puede pasar el puente.
Un pons asinorum en la geometría euclidiana sería el teorema de Pitágoras, que representa un conocimiento elemental en geometría, que se utilizó durante la Edad Media como prueba para evaluar la capacidad matemática de los estudiantes que se iban a dedicar a la docencia. La identificación del teorema de Pitágoras con el pons asinorum en matemáticas da testimonio la novela de Julio Verne (1828-1905) , De la Tierra a la Luna (1865), cuando Barbicane‑ intentando establecer comunicación con los selenitas- recordaba que años atrás un geómetra alemán propuso enviar una comisión de sabios a Siberia y desde allí representar, mediante faros luminosos, unas enormes figuras geométricas visibles desde el espacio exterior entre las que debía estar el teorema de Pitágoras…
“…Llamado del cuadrado de la hipotenusa y vulgarmente llamado Pons asinorum por los franceses…Todo ser inteligente ‑decía el geómetra‑ debe comprender el destino científico de esa figura. Los selenitas, si existen, responderán con una figura semejante, y, una vez establecida la comunicación, será sencillo crear un alfabeto que permita conversar con los habitantes de la Luna”
No obstante, en las universidades medievales, cuando se explicaba la geometría siguiendo los Elementos de Euclides el pons asinorum de la geometría más representativo no era el Teorema de Pitágoras, que es la Proposición 47 del libro I de los Elementos, sino a la proposición número 5, que dice que: los ángulos opuestos a los lados iguales de un triángulo isósceles, son también iguales.
Algunos autores suponen que, en realidad, el término fue acuñado en los años más oscuros de la Alta Edad Media, época en que las obras de referencia en matemáticas eran las obras de Boecio (475-524), pero el primer autor que recoge el término pons asinorum fue el profesor de la Universidad de París, entre 1480-1490, Pedro Tartareto, que se distinguió por sus comentarios a Aristóteles Expositio super textum Aristotelis (1514); Commentarium in Isagoges et libros logicorum Aristotelis (1494).
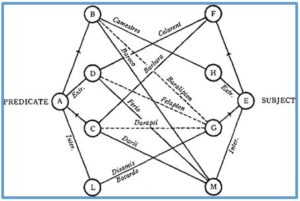
En el diccionario de Ferrater Mora (1912-1991) se recoge una definición más precisa; dice que Pons asinorum es el nombre que recibe la figura o diagrama mediante la cual se representan las relaciones necesarias para el descubrimiento del término medio en el silogismo, es decir, para descubrir la llamada inventio medii (descubrimiento del medio), que significa el hallazgo del camino o puente lógico, que relaciona la premisa inicial con la conclusión.
El primer pons asinorum de los Elementos de la geometría euclidiana es la proposición 5 del libro I y estaría formado por los pasos lógicos que permitían llegar hasta el enunciado que deseamos probar, partiendo de los postulados, las nociones comunes y las definiciones, que son base de la geometría euclidiana, así como y las proposiciones ya probadas. Es decir, las tablas del puente son los pasos lógicos y las proposiciones que utilizamos desde los principios hasta la proposición que pretendemos demostrar.
A continuación, se expone la Proposición 5 con los postulados, nociones comunes y proposiciones que utilizó Euclides para probarla, que constituyen, en suma, el Pons asinorum de esta proposición.
Proposición 5.- En los triángulos isósceles los ángulos de la base son iguales entre sí, y prolongadas las dos rectas iguales, los ángulos situados bajo la base serán iguales entre sí.
Demostración:

Sea ΑΒC el triángulo isósceles que tiene el lado ΑΒ igual al lado ΑC, y sean ΒD, CΕ el resultado de prolongar en línea recta las rectas ΑΒ, ΑC [Postulado 2]. Queremos probar que ∠ΑΒC=∠ΑCΒ y ∠CΒD =∠ΒCΕ. Tomemos al azar un punto F en la recta ΒD y quítese de ΑΕ, el segmento ΑG igual al ΑF [Prop 3. LibroI], y trácense las rectas FC, GΒ [Postulado 1]. Ahora bien, como ΑF=ΑG y ΑΒ=ΑC, entonces FΑ = GA, ΑC=AB y comprenden el ángulo común ∠FΑG; por tanto, FC = GΒ, y el triángulo △ΑFC será igual al triángulo △ΑGΒ, y los ángulos restantes subtendidos por lados iguales serán también iguales respectivamente, ∠ΑCF = ∠ΑΒG y ∠ΑFC =ΑGΒ [Prop 4. Libro I]. Como ΑF = AE, cuyas respectivas partes ΑΒ = ΑC, entonces ΒF = CG. Pero se ha demostrado también que FC = GΒ; entonces ΒF = CG, FC = GΒ, respectivamente; y ∠ΒFC=∠CGΒ y su base común es ΒC; y el triángulo △ΒFC será, por tanto, igual al triángulo △CGΒ, y los ángulos restantes subtendidos por lados iguales serán también iguales respectivamente; así que ∠FΒC=∠GCΒ y ∠ΒCF=∠CΒG. Así pues, como se ha demostrado que ∠ΑΒG = ∠ΑCF cuyas partes respectivas ∠CΒG =∠ΒCF, entonces ∠ΑΒC=∠ΑCΒ y están en la base del triángulo △ΑΒC. Pero se ha demostrado que también ∠FΒC=∠GCΒ; y son los situados debajo de la base. Q.E.D. (Quod Erat Demonstrandum)
Esta demostración muestra el camino seguido para probarla y es cierto que sorprende que un resultado visualmente tan evidente se expusiera de una forma aparentemente farragosa, esto es con un itinerario lógico tan largo. Y no es porque no se conocieran demostraciones más cortas partiendo de la igualdad de triángulos (utilizando, por ejemplo que dos triángulos son son iguales cuando tienen dos lados iguales e igual el ángulo comprendido entre ellos), pero Euclides optó por la demostración anterior, seguramente porque contribuía dar a sus discípulos un ejemplo del rigor de las demostraciones geométricas. Seguramente, habría optado por una demostración como la siguiente:
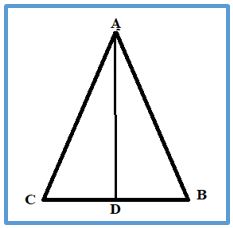
Proposición 5. Si en un triángulo dos lados son iguales, los ángulos opuestos a los lados también son iguales
Demostración. Supongamos que el triángulo △ABC tiene lados AB = AC iguales. Dibujar la bisectriz del ángulo ∠BAC, y sea D el punto donde la bisectriz corta al lado BC. Entonces los triángulos ABD y ACD tienen 2 lados Iguales y los ángulos comprendidos iguales. Luego por la [Prop 4. Libro I] los ángulos ∠ABD y ∠ACD son iguales.
Evidentemente esta demostración es más sencilla, pero con ella se aplican conceptos que no habían aparecido todavía en los Elementos cuando Euclides expuso la proposición 5 y la primera contribuye mas a fortalecer el rigor lógico en geometría de los estudiantes.
Y en los Elementos aparecen los conceptos con una estructura lógica deductiva. Tenemos que destacar que, a partir del siglo XVII, en la geometría euclidiana, con las demostraciones visuales, los métodos algebraicos y el triunfo del cálculo para describir el mundo físico el rigor lógico se fue relajando en favor de un criterio que venía a decir: si responde a la realidad física es válido. Pero eso es otra historia, que analizaremos más adelante.